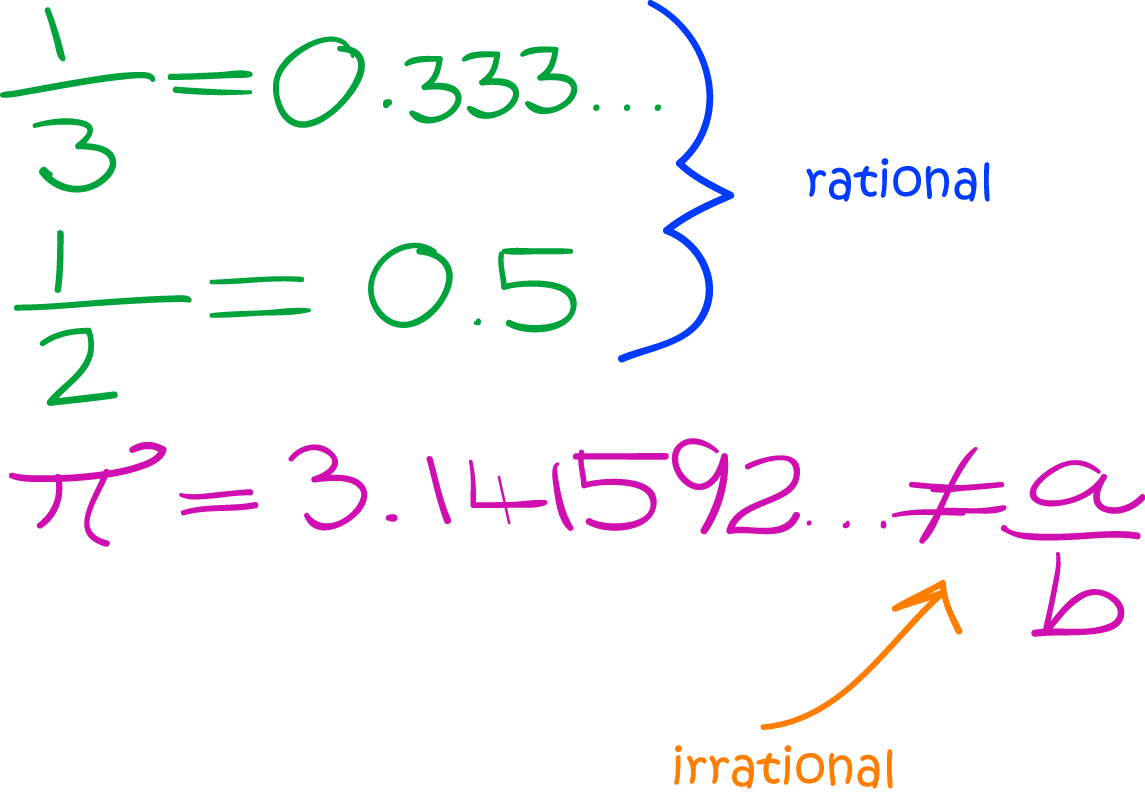Irrational numbers, a captivating concept in mathematics, often intrigue both students and mathematicians alike. These numbers, which cannot be expressed as simple fractions, open a world of endless decimal places that do not repeat. In essence, an irrational number is a number that cannot be written as a ratio of two integers, making it a vital component of real numbers.
Understanding irrational numbers is fundamental for delving deeper into the realms of mathematics. They are essential in various fields such as geometry, engineering, and computer science. The concept of irrational numbers dates back to the ancient Greeks, who discovered that numbers like the square root of 2 could not be expressed as a fraction, thus leading to the recognition of their irrationality.
In today's world, irrational numbers play a significant role in scientific calculations and theoretical mathematics. From the famous number π (pi) to the enigmatic number e, irrational numbers are intrinsic to many mathematical theories and applications. This article will explore the fascinating world of irrational numbers, providing a comprehensive understanding of their properties, significance, and real-world applications.
Table of Contents
- Definition and Characteristics of Irrational Numbers
- Historical Background of Irrational Numbers
- Famous Irrational Numbers and Their Importance
- How are Irrational Numbers Different from Rational Numbers?
- Real-World Applications of Irrational Numbers
- Importance of Irrational Numbers in Mathematics
- Can Irrational Numbers be Measured Precisely?
- Understanding Pi: The Most Famous Irrational Number
- The Mysterious Number e and Its Applications
- Why Do Irrational Numbers Matter in Today's World?
- Common Misconceptions About Irrational Numbers
- How to Approximate Irrational Numbers?
- Frequently Asked Questions
- Conclusion
Definition and Characteristics of Irrational Numbers
Irrational numbers are those that cannot be expressed as a simple fraction or ratio of two integers. Unlike rational numbers, which have a terminating or repeating decimal representation, irrational numbers continue indefinitely without repeating. Their uniqueness lies in their non-repetitive decimal expansion. A classic example of an irrational number is the square root of 2, which cannot be expressed as a fraction of two integers.
Several characteristics define irrational numbers:
- They cannot be expressed as a/b, where a and b are integers, and b is not zero.
- Their decimal expansions are non-terminating and non-repeating.
- They are part of the set of real numbers, which include both rational and irrational numbers.
Understanding these characteristics is essential to grasp the concept of irrational numbers fully. They play a pivotal role in various mathematical theories and applications, requiring a thorough comprehension of their properties.
Historical Background of Irrational Numbers
The history of irrational numbers dates back to ancient Greece. The early Greeks, including mathematicians like Pythagoras, initially believed that all numbers could be expressed as a ratio of integers. However, the discovery of the square root of 2, which cannot be expressed as a fraction, challenged this belief and led to the recognition of irrational numbers.
This discovery was monumental, as it expanded the understanding of numbers beyond the realm of integers and rational numbers. Over time, mathematicians like Euclid further explored these numbers, contributing to the development of number theory. The concept of irrationality was crucial for the advancement of mathematical thought and laid the foundation for modern mathematics.
Famous Irrational Numbers and Their Importance
Several irrational numbers have gained fame due to their significance in mathematics. Some of the most notable ones include:
- π (Pi): Arguably the most famous irrational number, pi is the ratio of a circle's circumference to its diameter. It is widely used in geometry, trigonometry, and calculus.
- e: Known as Euler's number, e is the base of the natural logarithm and is crucial in calculus and complex number theory.
- √2: The square root of 2 is a fundamental irrational number discovered by the Greeks, representing the diagonal of a square with side length 1.
These numbers are not only mathematically significant but also play a vital role in various scientific and engineering applications. Their importance cannot be overstated, as they are integral to many mathematical formulas and theories.
How are Irrational Numbers Different from Rational Numbers?
The primary distinction between irrational and rational numbers lies in their representation. Rational numbers can be expressed as a fraction of two integers (a/b), where b is not zero. Their decimal expansions are either terminating or repeating, making them predictable and easy to work with.
On the other hand, irrational numbers have non-terminating and non-repeating decimal expansions. This unpredictability makes them unique and sets them apart from rational numbers. While both types of numbers are part of the real number system, understanding their differences is crucial for differentiating between rational and irrational numbers effectively.
Real-World Applications of Irrational Numbers
Irrational numbers are not just theoretical constructs; they have practical applications in various fields:
- Geometry: The use of π in calculating the circumference and area of circles is a classic example of irrational numbers in geometry.
- Engineering: Engineers use irrational numbers in designing structures and systems, as they often appear in calculations involving curves and angles.
- Physics: Concepts like wave functions and quantum mechanics involve irrational numbers, highlighting their significance in understanding the physical world.
These applications demonstrate the utility and importance of irrational numbers in solving real-world problems and advancing scientific knowledge.
Importance of Irrational Numbers in Mathematics
In mathematics, irrational numbers are essential for the completeness of the real number system. They fill the gaps between rational numbers, ensuring that the number line is continuous. This continuity is vital for calculus and other areas of mathematics that rely on the concept of limits and infinite series.
Irrational numbers also contribute to the development of mathematical theories, such as transcendental number theory. Their properties and behaviors have been extensively studied, leading to a deeper understanding of mathematical concepts and principles.
Can Irrational Numbers be Measured Precisely?
While irrational numbers cannot be expressed as exact fractions, they can be approximated to a desired level of precision. This approximation is typically achieved using numerical methods or calculators capable of handling large decimal places.
Although exact measurement is impossible due to their non-repeating nature, irrational numbers can be represented with sufficient accuracy for practical purposes. This ability to approximate is crucial for their application in scientific and engineering calculations.
Understanding Pi: The Most Famous Irrational Number
Pi (π) is perhaps the most renowned irrational number, known for its appearance in the formula for the circumference of a circle (C = πd) and its area (A = πr²). Its decimal representation begins with 3.14159 and extends infinitely without repetition.
The significance of pi extends beyond geometry; it appears in various formulas across different mathematical disciplines, including calculus and trigonometry. Its properties have fascinated mathematicians for centuries, leading to numerous attempts to calculate its digits with increasing precision.
The Mysterious Number e and Its Applications
The number e, approximately equal to 2.71828, is another famous irrational number with significant applications. It serves as the base of the natural logarithm and is crucial in calculus, particularly in the study of exponential growth and decay.
Euler's number (e) is also fundamental in complex analysis and number theory. Its unique properties and applications make it an essential tool for mathematicians and scientists alike.
Why Do Irrational Numbers Matter in Today's World?
Irrational numbers are vital for modern mathematics and science, providing the foundation for numerous theories and applications. Their importance is evident in fields like physics, engineering, and computer science, where precise calculations and models are essential.
Their role in mathematical education is equally significant, as understanding irrational numbers is crucial for students to grasp advanced mathematical concepts. As such, they remain a fundamental aspect of the mathematical landscape, influencing both theoretical and practical advancements.
Common Misconceptions About Irrational Numbers
Despite their importance, irrational numbers are often misunderstood. Some common misconceptions include:
- Believing that irrational numbers cannot be represented numerically. While they cannot be expressed as exact fractions, they can be approximated with high precision.
- Assuming that all irrational numbers are complex. In reality, they are part of the real number system and exist on the number line alongside rational numbers.
Addressing these misconceptions is essential for fostering a clearer understanding of irrational numbers and their role in mathematics.
How to Approximate Irrational Numbers?
Approximating irrational numbers involves numerical methods that provide a close representation of their value. Common techniques include:
- Using decimal approximations, such as representing π as 3.14 or e as 2.72.
- Employing iterative algorithms for more precise calculations, often used in computational applications.
These approximations are crucial for applying irrational numbers in practical scenarios, where exact values are not necessary but high precision is required.
Frequently Asked Questions
- What is the difference between rational and irrational numbers?
Rational numbers can be expressed as a fraction of two integers, while irrational numbers cannot. Irrational numbers have non-repeating, non-terminating decimal expansions. - Are all square roots irrational numbers?
No, only square roots of non-perfect squares are irrational. For example, √2 is irrational, but √4 is rational since it equals 2. - Can irrational numbers be negative?
Yes, irrational numbers can be negative. For example, -√3 is an irrational number. - Do irrational numbers have any patterns?
While their decimal expansions do not repeat, some irrational numbers, like π, exhibit apparent randomness, but no predictable pattern. - Are there infinitely many irrational numbers?
Yes, there are infinitely many irrational numbers, as they fill the gaps between rational numbers on the number line. - Can irrational numbers be used in equations?
Yes, irrational numbers can be used in equations, often requiring approximation techniques for solutions.
Conclusion
Irrational numbers, with their non-repeating and non-terminating decimal expansions, are a cornerstone of mathematics. Their discovery and subsequent exploration have paved the way for significant advancements in mathematical theory and practice. From the ancient Greeks to modern-day mathematicians, irrational numbers continue to intrigue and inspire, proving their enduring relevance in both mathematical and real-world contexts.
Understanding what an irrational number is and its applications enhances our comprehension of mathematics, allowing for more accurate calculations and deeper insights into mathematical phenomena. As we continue to explore the vast landscape of numbers, irrational numbers remain a testament to the complexity and beauty of mathematics.