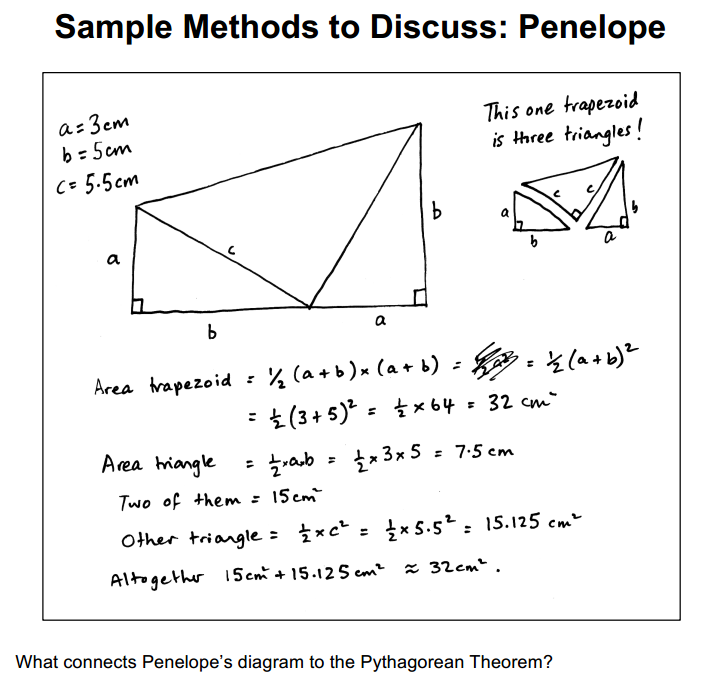
The Pythagorean Theorem is an essential cornerstone of mathematics, known to students and mathematicians alike. It forms the basis for understanding the relationships between the sides of a right-angled triangle. However, when we delve deeper into the theorem's complexities, we encounter what many consider the hardest Pythagorean theorem problem. This intricate problem challenges even the most advanced mathematical thinkers, pushing the boundaries of our understanding and application of this ancient geometric principle.
For centuries, the Pythagorean Theorem has been a fundamental tool in mathematics, allowing for the exploration of geometric shapes and the development of trigonometry. Despite its seemingly straightforward formulation, the theorem's applications extend far beyond simple triangle calculations. The hardest Pythagorean theorem problem represents a pinnacle of intellectual pursuit within this field, requiring a nuanced grasp of algebra, geometry, and number theory.
This article examines the complexities and nuances of the hardest Pythagorean theorem problem, providing a comprehensive overview of its significance and challenges. We will explore the historical context, delve into the mathematical intricacies, and discuss the implications of solving such a complex problem. By the end, readers will gain a deeper appreciation for the theorem's role in modern mathematics and the intellectual rigor required to tackle its most formidable challenges.
Table of Contents
- The Historical Context of the Pythagorean Theorem
- The Mathematical Foundations of the Pythagorean Theorem
- What Makes the Hardest Pythagorean Theorem Problem So Challenging?
- Real-World Applications and Implications
- Strategies for Solving Complex Pythagorean Problems
- The Role of Number Theory in Pythagorean Challenges
- Advanced Geometric Concepts in Pythagorean Problems
- Algebraic Techniques and the Pythagorean Theorem
- Famous Problems Related to the Pythagorean Theorem
- The Educational Importance of Pythagorean Problems
- Modern Research and the Pythagorean Theorem
- How Do Mathematicians Approach the Hardest Pythagorean Theorem Problem?
- Future Directions in Pythagorean Theorem Research
- FAQs
- Conclusion
The Historical Context of the Pythagorean Theorem
The Pythagorean Theorem, attributed to the ancient Greek mathematician Pythagoras, has been a fundamental concept in mathematics for over two millennia. Its discovery marked a significant milestone in the development of mathematical theory, influencing countless areas of study. The theorem states that in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. This simple yet profound insight laid the groundwork for the field of geometry and has been used in various applications throughout history.
Historical records suggest that the knowledge of this theorem predates Pythagoras, with evidence of its use in ancient Babylonian and Indian mathematics. However, Pythagoras and his followers were instrumental in formalizing the theorem and establishing its place in mathematical discourse. The Pythagorean Theorem became a cornerstone of Greek mathematics, influencing the works of later mathematicians such as Euclid and Archimedes.
The theorem's historical significance extends beyond its mathematical applications. It has been a symbol of the pursuit of knowledge and the human capacity for abstract thought. The Pythagorean Theorem represents a bridge between the tangible world of shapes and the abstract realm of numbers, highlighting the interconnectedness of different mathematical disciplines. Understanding the historical context of the theorem provides insight into its enduring relevance and the foundations of the hardest Pythagorean theorem problem.
The Mathematical Foundations of the Pythagorean Theorem
The Pythagorean Theorem is grounded in fundamental mathematical principles that have stood the test of time. Its formulation is both elegantly simple and profoundly powerful, allowing for a wide range of applications across various fields. The theorem's mathematical foundation is based on the properties of right-angled triangles, where the relationship between the sides can be expressed algebraically as a² + b² = c², with 'c' representing the hypotenuse.
This foundational equation is a manifestation of the geometric properties of right-angled triangles, providing a method for calculating unknown side lengths. The theorem's applicability extends to trigonometry, calculus, and even complex number theory, illustrating its versatility and importance in mathematics. The hardest Pythagorean theorem problem, therefore, builds upon these fundamental principles, challenging mathematicians to explore new depths of understanding and application.
In modern mathematics, the Pythagorean Theorem serves as a launching point for more advanced concepts, such as Pythagorean triples, which involve integer solutions to the equation. These mathematical explorations have yielded a wealth of knowledge, inspiring generations of mathematicians to push the boundaries of what is possible. The hardest Pythagorean theorem problem is a testament to the theorem's enduring complexity and relevance, inviting further exploration and discovery.
What Makes the Hardest Pythagorean Theorem Problem So Challenging?
The hardest Pythagorean theorem problem is challenging due to its intricate blend of mathematical concepts and the depth of understanding required to solve it. Unlike simple applications of the theorem, this problem demands a comprehensive grasp of algebra, geometry, and number theory, as well as the ability to synthesize these disciplines into a coherent solution.
One of the primary reasons for the problem's difficulty is the complexity of the mathematical relationships involved. Solving the hardest Pythagorean theorem problem requires an advanced understanding of Pythagorean triples, irrational numbers, and the properties of right-angled triangles. Additionally, the problem often involves large numbers or complex algebraic expressions, further complicating the solution process.
Another factor contributing to the problem's difficulty is the need for creative problem-solving and critical thinking skills. Mathematicians must approach the hardest Pythagorean theorem problem with an open mind, considering various strategies and techniques to arrive at a solution. This process often involves trial and error, as well as the ability to recognize patterns and relationships that may not be immediately apparent.
Real-World Applications and Implications
The Pythagorean Theorem and its associated problems have numerous real-world applications, highlighting the theorem's enduring relevance and importance. From engineering and architecture to physics and computer science, the theorem provides a foundation for understanding and solving complex problems in various fields.
In engineering, the Pythagorean Theorem is used to calculate distances and angles, essential for designing structures and machinery. Architects rely on the theorem to ensure the stability and balance of their designs, while physicists use it to analyze motion and forces. The hardest Pythagorean theorem problem, therefore, has implications for these fields, pushing the boundaries of what is possible and inspiring new innovations.
In computer science, the Pythagorean Theorem is applied to graphics and algorithms, enabling the development of sophisticated simulations and models. The hardest Pythagorean theorem problem can lead to advancements in these areas, challenging programmers to devise new solutions and algorithms. These real-world applications underscore the theorem's significance and the value of tackling its most challenging problems.
The Role of Number Theory in Pythagorean Challenges
Number theory plays a crucial role in the hardest Pythagorean theorem problem, providing a framework for understanding the properties of numbers and their relationships. This branch of mathematics is concerned with the study of integers and their properties, including divisibility, prime numbers, and modular arithmetic.
In the context of the hardest Pythagorean theorem problem, number theory helps mathematicians explore the properties of Pythagorean triples and the relationships between the sides of a right-angled triangle. By applying number theoretic techniques, mathematicians can uncover patterns and relationships that may not be immediately apparent, leading to potential solutions for the hardest Pythagorean theorem problem.
Number theory also provides insights into the nature of irrational numbers, which often play a role in complex Pythagorean problems. Understanding these numbers and their properties can help mathematicians devise new strategies for solving the hardest Pythagorean theorem problem, pushing the boundaries of mathematical knowledge and discovery.
Strategies for Solving Complex Pythagorean Problems
Solving the hardest Pythagorean theorem problem requires a combination of mathematical knowledge, creativity, and perseverance. Mathematicians must employ a variety of strategies to tackle the problem, drawing on their understanding of algebra, geometry, and number theory.
One effective strategy is to break the problem down into smaller, more manageable parts. By addressing each component individually, mathematicians can gain insights into the overall structure and relationships involved. This approach often involves identifying key patterns and relationships, which can serve as a basis for developing a solution.
- Use algebraic manipulation to simplify complex expressions.
- Apply geometric principles to understand the relationships between triangle sides.
- Explore number theoretic techniques to uncover patterns and relationships.
- Utilize computational tools to test hypotheses and verify solutions.
Ultimately, solving the hardest Pythagorean theorem problem requires a willingness to explore new ideas and approaches, as well as the ability to synthesize different mathematical concepts into a coherent solution. By employing these strategies, mathematicians can push the boundaries of their understanding and unlock new insights into this challenging problem.
Advanced Geometric Concepts in Pythagorean Problems
Advanced geometric concepts are often essential for tackling the hardest Pythagorean theorem problem, providing insights into the complex relationships between triangle sides and angles. These concepts extend beyond the basic properties of right-angled triangles, offering a deeper understanding of the theorem's applications and implications.
One such concept is the use of trigonometric identities, which can help mathematicians analyze the relationships between triangle angles and side lengths. By applying these identities, mathematicians can gain a more comprehensive understanding of the problem, uncovering new patterns and relationships that can inform potential solutions.
Other advanced geometric concepts, such as coordinate geometry and vector analysis, can also play a role in solving the hardest Pythagorean theorem problem. These tools allow mathematicians to visualize and manipulate geometric shapes in new ways, providing additional insights into the problem's structure and relationships.
Algebraic Techniques and the Pythagorean Theorem
Algebraic techniques are a crucial component of solving the hardest Pythagorean theorem problem, providing the tools necessary to manipulate and simplify complex expressions. By applying these techniques, mathematicians can gain insights into the problem's underlying structure and relationships, paving the way for potential solutions.
One common algebraic technique is the use of substitution, which involves replacing one expression with another to simplify the problem. This can help mathematicians identify key patterns and relationships, leading to a deeper understanding of the problem's intricacies.
- Substitution methods for simplifying equations.
- Factorization techniques to uncover hidden relationships.
- Use of algebraic identities to manipulate expressions.
Another powerful algebraic tool is factorization, which involves breaking down complex expressions into simpler components. By identifying common factors, mathematicians can gain insights into the problem's structure and relationships, potentially leading to a solution for the hardest Pythagorean theorem problem.
Famous Problems Related to the Pythagorean Theorem
Throughout history, the Pythagorean Theorem has inspired a variety of famous mathematical problems and puzzles, challenging mathematicians to push the boundaries of their understanding. These problems often involve complex relationships between numbers and geometric shapes, requiring a deep understanding of the theorem and its applications.
One such problem is Fermat's Last Theorem, which states that there are no whole number solutions to the equation xⁿ + yⁿ = zⁿ for n greater than 2. This problem, which remained unsolved for over 350 years, is closely related to the Pythagorean Theorem and highlights the complexity and intrigue of mathematical exploration.
Another famous problem is the Beal Conjecture, which extends the ideas of Fermat's Last Theorem to include solutions where the exponents are not necessarily equal. These problems, along with the hardest Pythagorean theorem problem, demonstrate the enduring fascination and challenge of the theorem, inspiring mathematicians to explore new ideas and approaches.
The Educational Importance of Pythagorean Problems
Pythagorean problems, including the hardest Pythagorean theorem problem, play a crucial role in mathematics education, providing students with opportunities to develop critical thinking and problem-solving skills. By engaging with these problems, students gain a deeper understanding of mathematical concepts and their applications, preparing them for future challenges in mathematics and beyond.
The hardest Pythagorean theorem problem, in particular, serves as a valuable learning tool, encouraging students to think creatively and explore new ideas. By tackling this challenging problem, students can develop a strong foundation in algebra, geometry, and number theory, as well as the ability to synthesize these disciplines into a coherent solution.
In addition to its educational value, the hardest Pythagorean theorem problem also serves as an inspiration for students, demonstrating the complexity and beauty of mathematics. By exploring the intricacies of this challenging problem, students can gain a deeper appreciation for the power and potential of mathematical exploration.
Modern Research and the Pythagorean Theorem
Modern research in mathematics continues to explore the complexities and applications of the Pythagorean Theorem, including the hardest Pythagorean theorem problem. Mathematicians are constantly pushing the boundaries of what is possible, uncovering new insights and developing innovative solutions to complex problems.
One area of research involves the use of computational tools and techniques to analyze and solve complex Pythagorean problems. By harnessing the power of computers, mathematicians can test hypotheses and verify solutions more efficiently, leading to potential breakthroughs in understanding and application.
Another area of research focuses on the connections between the Pythagorean Theorem and other branches of mathematics, such as topology and algebraic geometry. By exploring these connections, mathematicians can gain new insights into the theorem's implications and applications, potentially leading to advancements in a variety of fields.
How Do Mathematicians Approach the Hardest Pythagorean Theorem Problem?
Mathematicians approach the hardest Pythagorean theorem problem with a combination of mathematical knowledge, creativity, and perseverance. They employ a variety of strategies and techniques to tackle the problem, drawing on their understanding of algebra, geometry, and number theory.
One common approach is to break the problem down into smaller, more manageable parts, addressing each component individually to gain insights into the overall structure and relationships involved. This often involves identifying key patterns and relationships, which can serve as a basis for developing a solution.
Mathematicians also employ computational tools and techniques to test hypotheses and verify solutions, exploring new ideas and approaches to uncover potential solutions. By harnessing the power of computers, they can analyze complex Pythagorean problems more efficiently, leading to potential breakthroughs in understanding and application.
Future Directions in Pythagorean Theorem Research
The future of Pythagorean theorem research is bright, with mathematicians continuing to explore the complexities and applications of this fundamental mathematical concept. As new insights and solutions are uncovered, the potential for advancements in a variety of fields is vast.
One promising area of research involves the use of artificial intelligence and machine learning to analyze and solve complex Pythagorean problems. By harnessing the power of these technologies, mathematicians can gain new insights into the theorem's implications and applications, leading to potential breakthroughs in understanding and application.
Another area of exploration is the development of new mathematical techniques and approaches for tackling the hardest Pythagorean theorem problem. By pushing the boundaries of what is possible, mathematicians can uncover new insights and develop innovative solutions to complex problems, paving the way for future advancements in mathematics and beyond.
FAQs
What is the hardest Pythagorean theorem problem?
The hardest Pythagorean theorem problem is a complex mathematical challenge that involves advanced algebra, geometry, and number theory. It requires a deep understanding of Pythagorean triples, irrational numbers, and the properties of right-angled triangles.
Why is the hardest Pythagorean theorem problem significant?
This problem is significant because it pushes the boundaries of mathematical understanding and application. Solving it requires creativity, critical thinking, and a comprehensive grasp of multiple mathematical disciplines.
How does number theory relate to the hardest Pythagorean theorem problem?
Number theory provides a framework for understanding the properties of numbers and their relationships, which are essential for solving complex Pythagorean problems. It helps mathematicians explore Pythagorean triples and uncover patterns and relationships.
What strategies are used to solve the hardest Pythagorean theorem problem?
Mathematicians use a variety of strategies, including breaking the problem down into smaller parts, applying algebraic and geometric techniques, and using computational tools to test hypotheses and verify solutions.
How are advanced geometric concepts used in Pythagorean problems?
Advanced geometric concepts, such as trigonometric identities and coordinate geometry, help mathematicians analyze relationships between triangle angles and side lengths, providing insights into complex Pythagorean problems.
What are the future directions for Pythagorean theorem research?
Future research may involve the use of artificial intelligence, machine learning, and new mathematical techniques to analyze and solve complex Pythagorean problems, leading to advancements in understanding and application.
Conclusion
The hardest Pythagorean theorem problem represents a pinnacle of mathematical exploration, challenging even the most advanced thinkers to push the boundaries of their understanding. By delving into the complexities of this problem, mathematicians gain new insights into the fundamental principles of mathematics and their applications.
Through a combination of mathematical knowledge, creativity, and perseverance, mathematicians continue to uncover new solutions and innovations, paving the way for future advancements in mathematics and related fields. The hardest Pythagorean theorem problem serves as a testament to the enduring power and potential of mathematical exploration, inspiring future generations to explore the complexities of this fascinating topic.