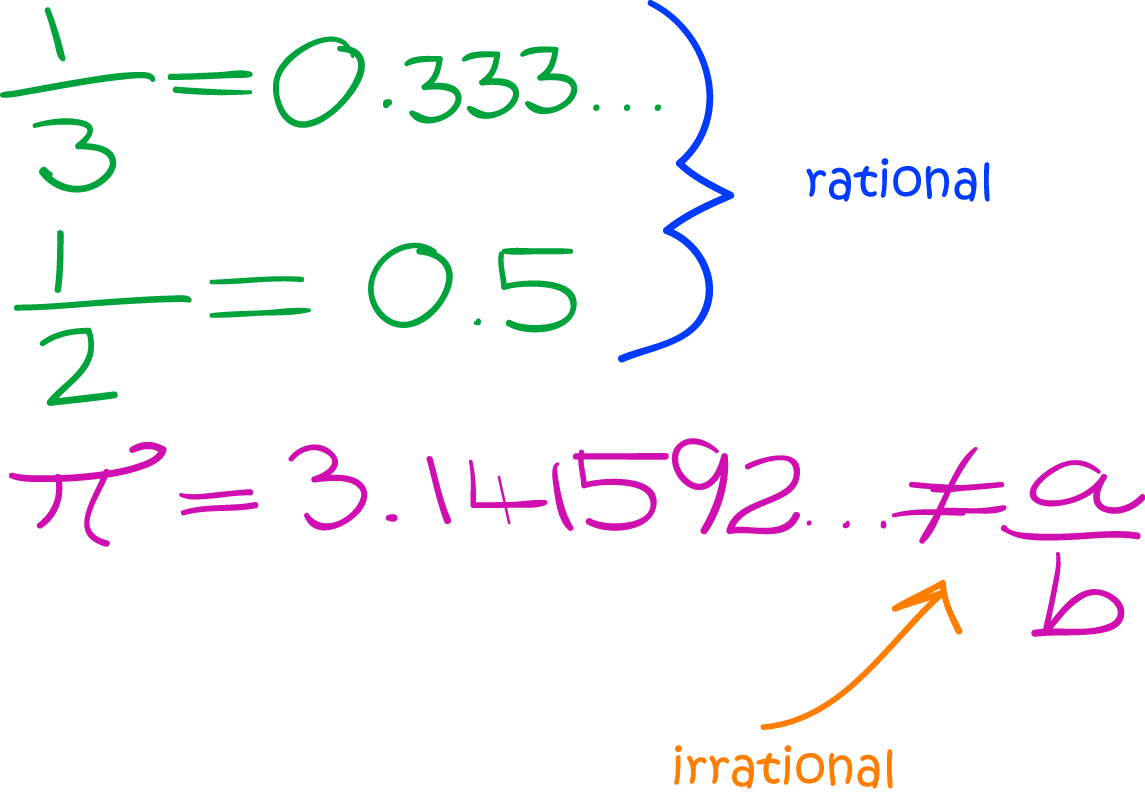In the realm of mathematics, numbers are the building blocks of all calculations and equations. Among these, irrational numbers hold a special place due to their unique properties and characteristics. These numbers, which cannot be expressed as a simple fraction, have fascinated mathematicians for centuries. But what exactly is an irrational number? How do they differ from their rational counterparts, and why are they important in mathematics?
Understanding irrational numbers is crucial for anyone delving into advanced mathematical concepts. These numbers, represented by non-repeating and non-terminating decimals, are often encountered in various mathematical problems and real-world scenarios. From the square root of a non-perfect square to the value of pi, irrational numbers are all around us, playing a vital role in scientific calculations, engineering, and even art.
In this comprehensive guide, we will explore the nature of irrational numbers, their history, and their significance in mathematics and beyond. We will delve into their properties, how they are identified, and their applications in different fields. By the end of this article, you will have a thorough understanding of what an irrational number is and why it is an essential concept to grasp.
Table of Contents
- What is an Irrational Number?
- How Do Irrational Numbers Differ from Rational Numbers?
- When Did Irrational Numbers First Appear in Mathematics?
- What Are the Key Properties of Irrational Numbers?
- Can You Provide Examples of Irrational Numbers?
- How to Identify an Irrational Number?
- Where Are Irrational Numbers Used in Real Life?
- Why is Pi Considered an Irrational Number?
- How Are Square Roots Related to Irrational Numbers?
- Do Irrational Numbers Have Infinite Length?
- How to Calculate with Irrational Numbers?
- Who Are Some Famous Mathematicians Associated with Irrational Numbers?
- What Challenges Do Irrational Numbers Present?
- How Are Irrational Numbers Taught in Schools?
- What is the Future of Research on Irrational Numbers?
- Frequently Asked Questions
- Conclusion
What is an Irrational Number?
An irrational number is a type of real number that cannot be expressed as a simple fraction, meaning it cannot be written as the ratio of two integers. This is because irrational numbers have non-repeating, non-terminating decimal expansions. A classic example of an irrational number is the square root of 2, which cannot be precisely expressed as a fraction and has an infinite decimal expansion.
Irrational numbers are essential in mathematics as they fill the gaps between rational numbers on the number line. While rational numbers are countable, irrational numbers are uncountable, indicating that there are infinitely more irrational numbers than rational numbers. This concept challenges our understanding of numbers and the continuum of the real number line.
Mathematically, an irrational number can be defined as a real number that is not rational. It cannot be expressed as a quotient of two integers, with the denominator not equal to zero. The decimal form of an irrational number goes on infinitely without repeating, which differentiates it from rational numbers.
How Do Irrational Numbers Differ from Rational Numbers?
The primary difference between irrational and rational numbers lies in their representation. Rational numbers can always be represented as a fraction, where both the numerator and the denominator are integers. Conversely, irrational numbers cannot be expressed in this way. The decimal expansion of a rational number either terminates after a finite number of digits or becomes periodic, repeating a particular sequence of digits indefinitely.
On the other hand, irrational numbers have decimal expansions that neither terminate nor become periodic. This means that the digits continue infinitely without forming a repeating pattern. Due to this characteristic, irrational numbers cannot be precisely represented on a standard number line using fractions, and they require special notation or approximations.
The distinction is not just theoretical but also practical. In computational mathematics and real-world applications, the inability to represent irrational numbers as fractions can lead to challenges in calculations and measurements. However, this unique property also makes irrational numbers a fascinating area of study in mathematical research and theory.
When Did Irrational Numbers First Appear in Mathematics?
The concept of irrational numbers has a rich history that dates back to ancient Greece. The discovery is often attributed to the Pythagoreans, a group of Greek mathematicians who believed that all numbers were rational, or could be expressed as the ratio of two integers. This belief was challenged when they encountered the square root of 2 while studying the diagonals of a square.
This discovery was shocking to the Pythagoreans, as it contradicted their fundamental belief in the omnipresence of rational numbers. The existence of numbers that could not be expressed as a ratio of two integers led to significant philosophical and mathematical debates at the time. The term "irrational" itself comes from the Latin word "irrationalis," meaning "not rational."
Over the centuries, the understanding of irrational numbers evolved. In the 17th century, mathematicians like John Wallis and Isaac Newton further explored these numbers, leading to the development of calculus and more advanced mathematical theories. Today, irrational numbers are a well-established part of mathematics, with their properties and applications studied extensively.
What Are the Key Properties of Irrational Numbers?
Irrational numbers possess several distinctive properties that set them apart from other types of numbers. Understanding these properties is crucial for grasping their role in mathematics:
- Non-repeating and non-terminating decimals: The decimal expansion of an irrational number goes on infinitely without repeating any sequence of digits.
- Cannot be expressed as a fraction: An irrational number cannot be written as the quotient of two integers.
- Density on the real number line: Between any two rational numbers, there is an infinite number of irrational numbers, demonstrating their density on the real number line.
- Algebraic and transcendental: Irrational numbers can be algebraic (solutions to polynomial equations with integer coefficients) or transcendental (not solutions to any such equation). Examples include the square root of 2 (algebraic) and pi (transcendental).
- Closure under addition and multiplication: The sum or product of two irrational numbers may be rational or irrational, depending on the specific numbers involved.
These properties highlight the complexity and intrigue of irrational numbers, making them a fundamental topic in both theoretical and applied mathematics.
Can You Provide Examples of Irrational Numbers?
Irrational numbers are found throughout mathematics and have many well-known examples. Some of the most famous irrational numbers include:
- Square root of 2 (√2): The length of the diagonal of a square with side length 1 is √2, an irrational number.
- Pi (π): The ratio of a circle's circumference to its diameter, approximately 3.14159, is irrational.
- Euler's number (e): The base of the natural logarithm, approximately 2.71828, is irrational.
- Golden ratio (φ): An irrational number approximately equal to 1.61803, often found in art and architecture.
- Square root of non-perfect squares: Any square root of a non-perfect square, such as √3, √5, or √7, is irrational.
These examples illustrate the diverse nature of irrational numbers and their occurrence in various mathematical and real-world contexts.
How to Identify an Irrational Number?
Identifying whether a number is irrational involves examining its decimal expansion and its representation as a fraction. Here are some methods to identify an irrational number:
- Decimal Expansion: Check if the decimal expansion of the number is non-terminating and non-repeating. If it is, the number is likely irrational.
- Fraction Representation: Determine if the number can be expressed as a fraction of two integers. If it cannot, it is irrational.
- Square Roots of Non-Perfect Squares: The square root of a non-perfect square is always irrational.
- Known Irrational Numbers: Recognize established irrational numbers like π, e, and the golden ratio (φ) as irrational.
Using these methods, one can identify irrational numbers in various mathematical problems and applications.
Where Are Irrational Numbers Used in Real Life?
Irrational numbers play a crucial role in many real-life applications, particularly in fields that require precise and accurate measurements. Here are some examples of where irrational numbers are used:
- Engineering and Architecture: The golden ratio (φ) is often used in design and architecture to create aesthetically pleasing structures.
- Science and Physics: Pi (π) is essential for calculations involving circles and waves, such as in engineering and physics.
- Finance and Economics: Euler's number (e) is used in calculating compound interest and growth rates.
- Computer Graphics: Irrational numbers are used in algorithms for rendering curves and shapes.
- Music and Acoustics: The frequency ratios of musical notes are often related to irrational numbers, affecting harmonics and acoustics.
These applications demonstrate the importance of understanding irrational numbers and their role in various scientific and practical contexts.
Why is Pi Considered an Irrational Number?
Pi (π) is perhaps the most famous irrational number, known for its endless decimal expansion and significance in geometry and mathematics. Pi is defined as the ratio of a circle's circumference to its diameter, and it is approximately equal to 3.14159. The proof of its irrationality was first established by Johann Lambert in the 18th century.
The irrationality of pi means that it cannot be expressed as a simple fraction, and its decimal expansion does not repeat or terminate. This property makes pi an essential concept in various mathematical calculations, especially those involving circles, such as calculating the area (πr²) and circumference (2πr) of a circle.
Pi's irrationality also extends to its transcendental nature, meaning it is not a solution to any algebraic equation with integer coefficients. This transcendental property further underscores the complexity and importance of pi in mathematical theory and applications.
How Are Square Roots Related to Irrational Numbers?
Square roots are closely related to irrational numbers, particularly when dealing with non-perfect squares. A non-perfect square is a number that cannot be expressed as the square of an integer. The square root of a non-perfect square is always irrational, as it cannot be precisely represented as a fraction.
For example, the square root of 2 (√2) is irrational because it cannot be expressed as a simple fraction. Its decimal expansion is non-repeating and non-terminating, approximately equal to 1.41421. Similarly, the square roots of 3, 5, 7, and other non-perfect squares are irrational.
The relationship between square roots and irrational numbers is fundamental in mathematics, particularly in algebra and geometry. Understanding this relationship allows mathematicians and scientists to solve complex equations and analyze geometric shapes and patterns.
Do Irrational Numbers Have Infinite Length?
Yes, irrational numbers have an infinite decimal length. This means their decimal expansion continues indefinitely without terminating or repeating a sequence of digits. This infinite length is a defining characteristic of irrational numbers, setting them apart from rational numbers, which have finite or repeating decimal expansions.
Due to their infinite length, irrational numbers cannot be precisely represented in numerical form. Instead, they are often approximated using a limited number of decimal places for practical calculations. For example, pi (π) is commonly approximated as 3.14159, although its true decimal expansion goes on forever.
The infinite nature of irrational numbers presents both challenges and opportunities in mathematics and science. It challenges our understanding of numbers and their representation, while also providing opportunities for exploration and discovery in mathematical theory and research.
How to Calculate with Irrational Numbers?
Calculating with irrational numbers involves understanding their properties and using approximations when necessary. Here are some tips for working with irrational numbers:
- Use Approximations: In practical calculations, use approximations of irrational numbers to a limited number of decimal places.
- Algebraic Expressions: Represent irrational numbers in algebraic expressions where possible, such as using √2 instead of its decimal approximation.
- Use Calculators: Use scientific calculators or software to perform calculations involving irrational numbers accurately.
- Understand Limitations: Be aware of the limitations of approximations and the potential for rounding errors in calculations.
By understanding these techniques, one can effectively work with irrational numbers in mathematical problems and real-world applications.
Who Are Some Famous Mathematicians Associated with Irrational Numbers?
Several famous mathematicians have contributed to the understanding and study of irrational numbers. Some notable figures include:
- Pythagoras: The Pythagorean theorem led to the discovery of irrational numbers, particularly the square root of 2.
- Johann Lambert: Lambert proved the irrationality of pi in the 18th century, a significant milestone in the study of irrational numbers.
- Georg Cantor: Cantor's work on set theory and the concept of infinity contributed to the understanding of irrational numbers' density on the real number line.
- Joseph Liouville: Liouville was the first to provide a construction of a transcendental number, furthering the study of irrational numbers.
These mathematicians and their contributions have shaped our understanding of irrational numbers and their role in mathematics.
What Challenges Do Irrational Numbers Present?
Irrational numbers present several challenges in mathematics and real-world applications. Some of these challenges include:
- Precision: The infinite decimal expansion of irrational numbers makes precise calculations difficult, requiring approximations.
- Representation: Irrational numbers cannot be expressed as simple fractions, complicating their representation in mathematical equations.
- Computation: Calculating with irrational numbers can lead to rounding errors and inaccuracies in numerical and scientific computations.
Despite these challenges, irrational numbers are essential in mathematics and science, offering opportunities for exploration and discovery in mathematical theory and research.
How Are Irrational Numbers Taught in Schools?
Irrational numbers are typically introduced in middle or high school mathematics curricula. Teachers use various methods to explain the concept, such as:
- Visual Aids: Using number lines and geometric representations to illustrate the concept of irrational numbers.
- Examples: Providing examples of well-known irrational numbers, such as √2 and π, to demonstrate their properties.
- Activities: Engaging students in activities and exercises to identify and approximate irrational numbers.
By using these teaching methods, educators can help students understand the concept of irrational numbers and their significance in mathematics.
What is the Future of Research on Irrational Numbers?
The study of irrational numbers continues to be an active area of research in mathematics and related fields. Some potential areas of future research include:
- Advanced Theories: Exploring advanced mathematical theories and concepts related to irrational numbers, such as transcendental numbers and their properties.
- Computational Methods: Developing new computational methods and algorithms to accurately calculate with irrational numbers.
- Applications: Investigating new applications of irrational numbers in science, technology, and engineering.
As researchers continue to explore these areas, the understanding and application of irrational numbers will likely expand, leading to new discoveries and innovations.
Frequently Asked Questions
1. Can irrational numbers be negative?
Yes, irrational numbers can be negative. For example, -√2 is a negative irrational number.
2. Is zero an irrational number?
No, zero is not an irrational number. It is a rational number because it can be expressed as a fraction (0/1).
3. How do you add and subtract irrational numbers?
Adding and subtracting irrational numbers follows the same rules as rational numbers. However, the result may be rational or irrational depending on the numbers involved.
4. Are all square roots irrational?
No, not all square roots are irrational. The square root of a perfect square, such as √4 or √9, is rational.
5. Can two irrational numbers add up to a rational number?
Yes, two irrational numbers can add up to a rational number. For example, √2 and -√2 add up to 0, a rational number.
6. Is the sum of two irrational numbers always irrational?
No, the sum of two irrational numbers is not always irrational. It can be rational, as shown in the previous example.
Conclusion
Understanding what an irrational number is and its significance is fundamental to grasping more advanced mathematical concepts. These numbers, with their non-repeating and non-terminating decimal expansions, challenge our understanding of mathematics and the number line. They are essential in various mathematical problems and real-world applications, from engineering and architecture to science and finance.
By exploring the properties, history, and applications of irrational numbers, we gain insight into their importance and the role they play in mathematics and beyond. As research continues, the study of irrational numbers will likely lead to new discoveries and innovations, further expanding our understanding of mathematics and its applications.