The relationship between speed, distance, and time is one of the fundamental concepts in physics and mathematics. It helps us understand how objects move and interact with their environment. This relationship is encapsulated in a simple yet powerful formula, which is used in a variety of fields, including transportation, sports, and even space exploration. Understanding this formula is crucial for anyone looking to grasp the basics of motion and kinematics.

In essence, the formula that relates speed, distance, and time is a mathematical equation that allows us to calculate one of these variables when the other two are known. This equation is integral to solving real-world problems, such as determining travel time, calculating the distance covered by a moving object, or even estimating the speed required to reach a certain destination within a specific timeframe. By mastering this formula, one can make informed decisions based on accurate predictions and analysis.

In this article, we will delve deep into the intricacies of the speed, distance, and time formula. We will explore its components, applications, and limitations. Additionally, we will address some common questions and misconceptions surrounding this equation, providing a comprehensive understanding of its significance and utility. Whether you're a student, a professional, or simply someone with a keen interest in the mechanics of motion, this guide is designed to equip you with the knowledge you need to navigate the world of speed, distance, and time.

What is the formula for speed, distance, and time?
How does the speed, distance, and time formula work?
How to calculate speed?
Calculating distance
Determining time
Real-world applications
Limitations of the formula
Formula in different systems
Common misconceptions
Importance in education
Relation to acceleration and deceleration
Technological advancements
Frequently Asked Questions
Conclusion

What is the formula for speed, distance, and time?

The formula that encapsulates the relationship between speed, distance, and time is expressed mathematically as:

Speed = Distance / Time
Distance = Speed × Time
Time = Distance / Speed

This fundamental formula is derived from the basic definition of speed, which is the rate at which an object covers a certain distance over a period of time. It's a straightforward equation that forms the basis of more complex calculations in physics and engineering.

How does the speed, distance, and time formula work?

The formula works by establishing a proportional relationship between speed, distance, and time. When two of these variables are known, the third can be easily calculated. This is particularly useful in scenarios where one needs to determine how long a journey will take, how far an object has traveled, or what speed is necessary to reach a destination within a given timeframe.

For example, if a car travels at a speed of 60 kilometers per hour for 2 hours, the distance covered can be calculated using the formula:

Distance = Speed × Time = 60 km/h × 2 h = 120 km

This equation remains consistent across different units of measurement, whether in kilometers per hour, miles per hour, or meters per second, as long as the units are appropriately converted and matched.

How to calculate speed?

Calculating speed involves determining how fast an object is moving. To do this, one needs to know the distance covered and the time taken to cover that distance. The formula for calculating speed is:

Speed = Distance / Time

For instance, if a cyclist covers a distance of 30 kilometers in 2 hours, the speed can be calculated as:

Speed = 30 km / 2 h = 15 km/h

In this example, the cyclist is traveling at a speed of 15 kilometers per hour. This calculation is crucial in various contexts, such as determining the average speed of a vehicle, optimizing travel routes, and enhancing performance in sports and athletics.

Calculating distance

To calculate distance, one needs to know the speed at which an object is moving and the time it has been moving. The formula for calculating distance is:

Distance = Speed × Time

For example, if a train is moving at a speed of 80 kilometers per hour for 3 hours, the distance covered is:

Distance = 80 km/h × 3 h = 240 km

This calculation is fundamental in planning trips, estimating fuel consumption, and understanding the dynamics of motion in various contexts.

Determining time

Determining the time taken for a journey involves knowing the distance and the speed at which an object is moving. The formula for calculating time is:

Time = Distance / Speed

For instance, if a runner covers 10 kilometers at a speed of 5 kilometers per hour, the time taken can be calculated as:

Time = 10 km / 5 km/h = 2 hours

Calculating time is essential for efficient scheduling, optimizing travel plans, and understanding the temporal aspects of motion.

Real-world applications

The formula for speed, distance, and time has a wide range of real-world applications. Some of these include:

Transportation: Calculating travel times, optimizing routes, and estimating fuel consumption.
Sports: Analyzing athlete performance, determining race times, and enhancing training programs.
Engineering: Designing efficient transportation systems and understanding the mechanics of moving objects.
Astronomy: Calculating the speed and distance of celestial bodies.

These applications highlight the versatility and significance of the speed, distance, and time formula in various fields.

Limitations of the formula

While the speed, distance, and time formula is a powerful tool, it has its limitations. Some of these include:

Assumption of constant speed: The formula assumes that speed remains constant throughout the journey, which may not always be the case in real-world scenarios.
Neglect of external factors: The formula does not account for external factors such as weather conditions, terrain, and traffic, which can affect the actual speed and time taken.
Limited to linear motion: The formula is primarily applicable to linear motion and may not be suitable for calculating motion along curved paths.

Understanding these limitations is crucial for applying the formula accurately in practical situations.

Formula in different systems

The speed, distance, and time formula can be adapted to different measurement systems, such as the metric and imperial systems. In the metric system, speed is typically measured in kilometers per hour (km/h) or meters per second (m/s), while distance is measured in kilometers (km) or meters (m). In the imperial system, speed is often measured in miles per hour (mph), and distance in miles.

Converting between these units is essential for accurate calculations, especially when dealing with international data or traveling across regions with different measurement systems.

Common misconceptions

There are several misconceptions surrounding the speed, distance, and time formula. Some of these include:

Belief that speed is always constant: In reality, speed can fluctuate due to various factors such as traffic and road conditions.
Confusion between speed and velocity: While speed is a scalar quantity, velocity is a vector quantity that includes direction.
Misinterpretation of units: Incorrectly matching units of speed, distance, and time can lead to inaccurate calculations.

Addressing these misconceptions is vital for a clear understanding of the formula and its applications.

Importance in education

The speed, distance, and time formula is an essential component of mathematics and physics education. It provides students with a practical understanding of motion and helps develop problem-solving skills. By mastering this formula, students can apply mathematical concepts to real-world scenarios, enhancing their analytical and critical thinking abilities.

Incorporating this formula into the curriculum also prepares students for advanced studies in fields such as engineering, physics, and transportation sciences.

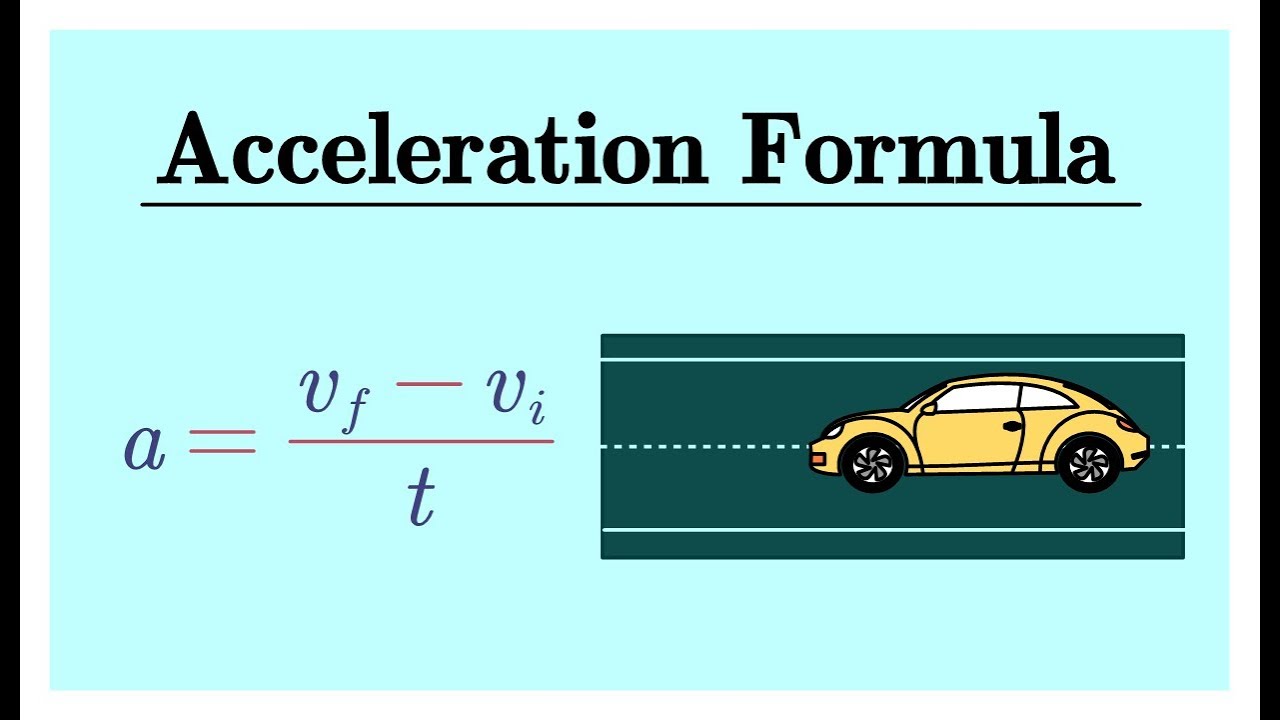
Relation to acceleration and deceleration

While the speed, distance, and time formula focuses on constant speed, it lays the foundation for understanding acceleration and deceleration. Acceleration refers to the rate of change of speed over time, while deceleration is the reduction of speed. These concepts are crucial for analyzing motion in dynamic systems, such as vehicles and machinery.

Understanding the relationship between speed, distance, and time is the first step toward comprehending more complex motion equations involving acceleration and deceleration.

Technological advancements

Technological advancements have enhanced our ability to measure and calculate speed, distance, and time with precision. GPS technology, for example, allows for real-time tracking of vehicles and accurate estimation of travel times. In sports, wearable devices provide athletes with detailed data on their performance, helping them optimize their training and improve their results.

These advancements underscore the continued relevance and importance of the speed, distance, and time formula in modern society.

Frequently Asked Questions

What is the basic formula for speed, distance, and time?
The basic formula is Speed = Distance / Time, allowing you to calculate any of the three variables if the other two are known.
How can I convert speed from km/h to m/s?
To convert speed from km/h to m/s, divide the value by 3.6.
What are some common units used for speed?
Common units include kilometers per hour (km/h), meters per second (m/s), and miles per hour (mph).
Can the formula be used for curved motion?
The formula is primarily designed for linear motion and may not be directly applicable to curved paths without additional calculations.
What factors can affect speed, distance, and time calculations?
Factors include weather conditions, road terrain, vehicle efficiency, and traffic.
Is the formula applicable in space travel?
Yes, the formula is used in space travel to calculate distances and travel times between celestial bodies, although additional factors like gravitational forces are considered.

Conclusion

The formula relating speed, distance, and time is an indispensable tool in both education and practical applications. By providing a clear understanding of motion, it enables individuals to solve problems, make informed decisions, and appreciate the dynamics of the world around them. Despite its simplicity, this formula serves as the foundation for more advanced studies in physics and engineering, highlighting its enduring relevance and utility in a rapidly evolving technological landscape.