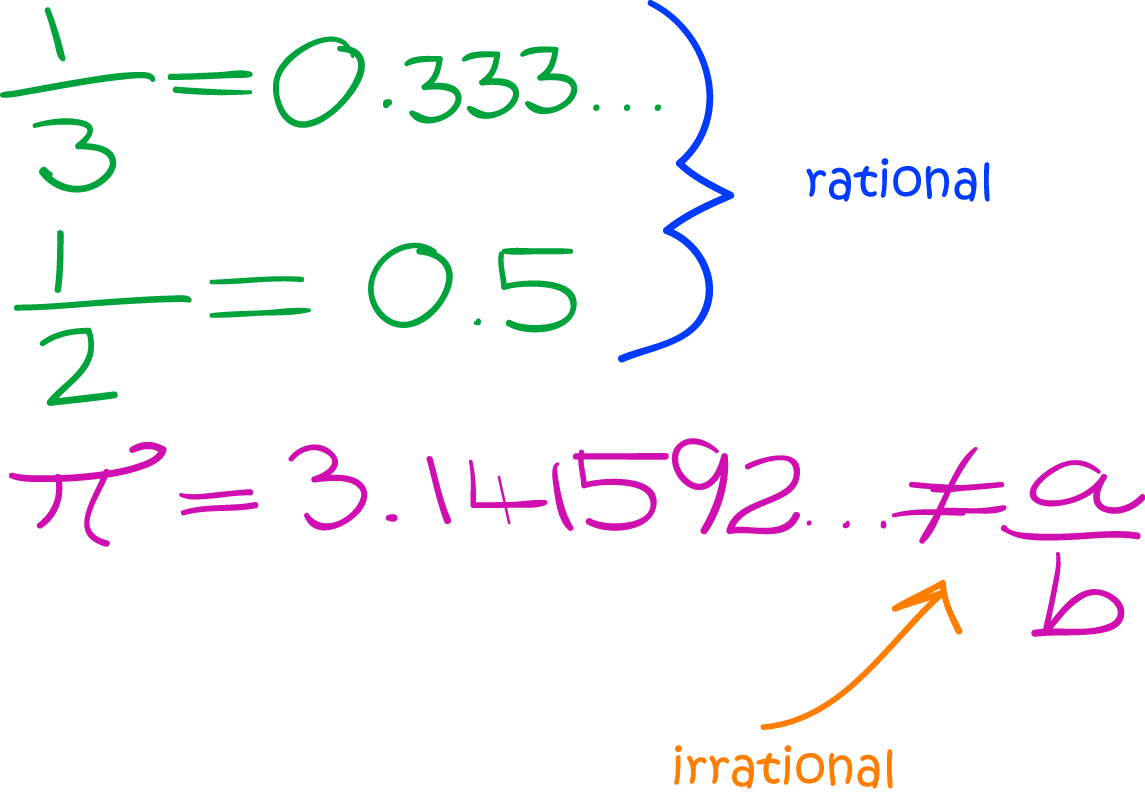Have you ever stumbled upon the concept of irrational numbers and wondered what they truly represent? These enigmatic entities are numbers that cannot be expressed as simple fractions, and they hold a significant place in the world of mathematics. The term 'irrational' might suggest chaos or randomness, but these numbers exhibit fascinating patterns and structures. From the square root of 2 to the elusive Pi, irrational numbers are everywhere, influencing fields as diverse as geometry, calculus, and even quantum physics.
In the grand tapestry of mathematics, irrational numbers weave a thread that challenges our understanding of numerical relationships. Unlike their rational counterparts, which can be neatly expressed as a ratio of integers, irrational numbers possess an infinite, non-repeating decimal expansion. This intriguing quality makes them both mysterious and essential, as they fill the gaps between rational numbers on the number line, creating a continuous and unbroken sequence of real numbers.
As we delve deeper into the world of irrational numbers, we'll explore their history, properties, and numerous examples that illustrate their importance. Along the way, we'll uncover their applications in various scientific disciplines and answer some common questions. By the end of the journey, you'll gain a newfound appreciation for these numerical wonders and their role in shaping the mathematical landscape.
Table of Contents
- What Are Irrational Numbers?
- Historical Context of Irrational Numbers
- Key Properties of Irrational Numbers
- Famous Examples of Irrational Numbers
- Why is Pi an Irrational Number?
- Exploring Euler's Number: Another Irrational Marvel
- The Golden Ratio: An Aesthetic Irrational Number
- Other Intriguing Irrational Number Examples
- How Do Irrational Numbers Arise in Mathematics?
- Applications of Irrational Numbers in Real Life
- How Are Irrational Numbers Taught in Schools?
- Common Misconceptions About Irrational Numbers
- Comparison: Rational vs. Irrational Numbers
- Frequently Asked Questions
- Conclusion
What Are Irrational Numbers?
Irrational numbers are a class of real numbers that cannot be expressed as a ratio of two integers. In simpler terms, they cannot be written as a fraction where both the numerator and the denominator are whole numbers. This characteristic sets them apart from rational numbers, which can be expressed in such a manner. The decimal expansion of irrational numbers is infinite and non-repeating, making them an intriguing subject of study in mathematics.
Origin of the Term "Irrational"
The term "irrational" comes from the Latin word 'irrationalis,' meaning "not rational." Historically, it was used to describe numbers that did not follow the conventional rules of arithmetic that applied to whole numbers and fractions. The Greeks were among the first to study such numbers, particularly through the work of mathematicians like Pythagoras and Hippasus.
Real Number Line and Irrational Numbers
On the real number line, irrational numbers fill the "gaps" between rational numbers, ensuring the continuity of the line. This concept is crucial in calculus and analysis, where the completeness of the real numbers is a foundational principle. Irrational numbers help to create a seamless transition from one point on the line to another, highlighting their importance in mathematical theory.
Decimal Expansion of Irrational Numbers
The decimal representation of an irrational number does not terminate and does not repeat. This infinite, non-repeating nature is what distinguishes them from rational numbers, which either terminate or have a repeating decimal pattern. For example, the number Pi (π) is famously known for its endless, non-repeating decimal expansion.
Historical Context of Irrational Numbers
The history of irrational numbers dates back to ancient Greece, where the Pythagorean school first encountered them through the study of geometry. The discovery of irrational numbers was initially met with resistance, as it challenged the Pythagorean belief that all numbers could be expressed as ratios of whole numbers.
The Pythagorean Discovery
The Pythagoreans discovered the existence of irrational numbers while attempting to calculate the diagonal of a square. They found that the diagonal of a square with side length 1 could not be expressed as a simple fraction, leading to the realization that such numbers existed beyond the realm of rational numbers.
The Story of Hippasus
Hippasus, a member of the Pythagorean school, is often credited with the discovery of irrational numbers. According to legend, he was drowned at sea for revealing the existence of irrational numbers, as it contradicted the belief that all numbers could be expressed as ratios. This tale highlights the revolutionary nature of the discovery and the initial resistance to accepting irrational numbers.
Key Properties of Irrational Numbers
Irrational numbers possess several unique properties that distinguish them from rational numbers. Understanding these properties is crucial for comprehending their role in mathematics.
Non-repeating and Non-terminating Decimals
One of the most defining properties of irrational numbers is their non-repeating and non-terminating decimal expansions. This means that their decimal representation continues infinitely without any recurring pattern, making them distinct from rational numbers.
Closure Under Addition and Multiplication
Irrational numbers are not closed under addition or multiplication, meaning that the sum or product of two irrational numbers may be rational. For example, the sum of the irrational numbers √2 and -√2 is 0, which is rational.
Density on the Number Line
Irrational numbers are densely packed on the real number line, meaning that between any two rational numbers, there exists an infinite number of irrational numbers. This property ensures the completeness of the real number line and is fundamental to the study of calculus and real analysis.
Transcendental Numbers
Many irrational numbers are also transcendental, meaning they are not solutions to any non-zero polynomial equation with rational coefficients. Famous examples of transcendental numbers include Pi (π) and Euler's number (e), both of which are irrational.
Famous Examples of Irrational Numbers
Several irrational numbers have become famous due to their significance in mathematics and their intriguing properties. These numbers often appear in various mathematical contexts, highlighting their importance.
The Number Pi (π)
Perhaps the most famous irrational number, Pi (π) represents the ratio of a circle's circumference to its diameter. Its decimal expansion is infinite and non-repeating, and it plays a crucial role in geometry, trigonometry, and calculus.
Euler's Number (e)
Euler's number (e) is another well-known irrational number that arises in the study of exponential growth and calculus. It is the base of natural logarithms and is used extensively in mathematical modeling and analysis.
The Golden Ratio (φ)
The Golden Ratio (φ) is an irrational number that appears in various contexts, from art and architecture to nature and biology. Its unique properties make it aesthetically pleasing, and it is often associated with beauty and harmony.
The Square Root of 2
The square root of 2 is one of the earliest discovered irrational numbers and is often used as an example in mathematical discussions. It represents the diagonal length of a square with side length 1 and cannot be expressed as a simple fraction.
Why is Pi an Irrational Number?
Pi (π) is an irrational number because its decimal expansion is infinite and non-repeating. This characteristic arises from its definition as the ratio of a circle's circumference to its diameter. Since this ratio cannot be accurately expressed as a fraction, Pi is classified as irrational.
Historical Calculations of Pi
The quest to calculate Pi has fascinated mathematicians for centuries. Ancient civilizations, including the Babylonians and Egyptians, developed approximations of Pi, but it was not until the advent of calculus that more accurate calculations were possible. Today, Pi is known to billions of decimal places, thanks to modern computational techniques.
Applications of Pi in Mathematics
Pi is used extensively in mathematics, particularly in geometry and trigonometry. It appears in formulas for calculating the area and circumference of circles, as well as in trigonometric functions and Fourier analysis. Pi also has applications in physics, engineering, and statistics.
Exploring Euler's Number: Another Irrational Marvel
Euler's number (e) is a fundamental constant in mathematics, known for its irrationality and its role in exponential growth. It is approximately equal to 2.71828 and is the base of natural logarithms.
Definition and Properties of Euler's Number
Euler's number is defined as the limit of (1 + 1/n)^n as n approaches infinity. This definition highlights its connection to exponential growth and compound interest, making it an essential constant in calculus and mathematical modeling.
Applications of Euler's Number
Euler's number is used in various fields, including finance, biology, and physics. It is essential for modeling exponential growth and decay, calculating compound interest, and solving differential equations. Its properties also make it a key component of the exponential function and natural logarithms.
The Golden Ratio: An Aesthetic Irrational Number
The Golden Ratio (φ) is an irrational number that is approximately equal to 1.61803. It is often associated with beauty and harmony, as it appears in various natural and human-made structures.
Mathematical Definition of the Golden Ratio
The Golden Ratio is defined as the positive solution to the quadratic equation x^2 - x - 1 = 0. This equation reflects the unique property of the Golden Ratio, where the ratio of the whole to the larger part is the same as the ratio of the larger part to the smaller part.
Occurrence of the Golden Ratio in Nature and Art
The Golden Ratio appears in various natural phenomena, including the arrangement of leaves on a stem, the branching patterns of trees, and the spiral patterns of shells. It is also used in art and architecture, where it is believed to create aesthetically pleasing proportions.
Other Intriguing Irrational Number Examples
Beyond the famous examples of Pi, Euler's number, and the Golden Ratio, there are numerous other irrational numbers that play significant roles in mathematics and science.
The Square Root of 3
The square root of 3 is another example of an irrational number, often used in geometry and trigonometry. It represents the height of an equilateral triangle with side length 2 and cannot be expressed as a simple fraction.
The Natural Logarithm of 2
The natural logarithm of 2 is an irrational number that arises in the study of logarithmic functions. It is used in various mathematical calculations and has applications in fields such as information theory and thermodynamics.
How Do Irrational Numbers Arise in Mathematics?
Irrational numbers arise in mathematics through various processes, including geometry, algebra, and calculus. Their occurrence often highlights the limitations of rational numbers and the need for a more comprehensive understanding of numerical relationships.
Geometric Constructions
Many irrational numbers arise from geometric constructions, such as the calculation of diagonals and angles. For example, the square root of 2 is derived from the diagonal of a square, while Pi is related to the circumference of a circle.
Algebraic Equations
Irrational numbers can also be solutions to algebraic equations that do not have rational solutions. These numbers often emerge when solving quadratic and higher-order polynomial equations, highlighting their importance in algebra.
Limits and Calculus
The study of limits and calculus often leads to the discovery of irrational numbers, particularly in the context of exponential growth and trigonometric functions. Euler's number (e) and Pi are prime examples of irrational numbers that arise from calculus.
Applications of Irrational Numbers in Real Life
Irrational numbers have numerous applications in real life, influencing fields ranging from science and engineering to art and design. Their unique properties make them essential for various practical and theoretical purposes.
Engineering and Architecture
Irrational numbers are used in engineering and architecture to design structures with precise proportions and dimensions. The Golden Ratio, in particular, is often employed to create aesthetically pleasing designs that are both functional and beautiful.
Science and Technology
In science, irrational numbers are used to model complex phenomena and solve intricate problems. Pi, for example, is essential for calculating circular and spherical measurements, while Euler's number is used in modeling exponential growth and decay.
Art and Design
The Golden Ratio is a popular tool in art and design, where it is used to create compositions with harmonious proportions. Many artists and designers incorporate the Golden Ratio into their work to achieve a sense of balance and beauty.
How Are Irrational Numbers Taught in Schools?
Teaching irrational numbers in schools involves introducing students to their properties and significance in mathematics. Educators employ various strategies to help students understand these complex numbers and their applications.
Conceptual Understanding
Teachers focus on helping students develop a conceptual understanding of irrational numbers, emphasizing their non-repeating decimal expansions and their distinction from rational numbers. Visual aids and interactive activities are often used to illustrate these concepts.
Real-life Examples
Educators use real-life examples, such as the calculation of circular measurements and the design of aesthetically pleasing structures, to demonstrate the relevance of irrational numbers. These examples help students see the practical applications of these numbers in everyday life.
Problem-solving Activities
Problem-solving activities are used to reinforce students' understanding of irrational numbers. These activities often involve geometric constructions, algebraic equations, and calculus problems that highlight the occurrence of irrational numbers.
Common Misconceptions About Irrational Numbers
Despite their significance, irrational numbers are often misunderstood. Addressing common misconceptions can help students and learners develop a more accurate understanding of these numbers.
Misconception: Irrational Numbers Are Random
One common misconception is that irrational numbers are random or chaotic. In reality, irrational numbers have specific properties and patterns, even though their decimal expansions do not repeat.
Misconception: All Non-repeating Decimals Are Irrational
Another misconception is that all non-repeating decimals are irrational. However, some non-repeating decimals, such as those generated by certain mathematical processes, can be rational.
Comparison: Rational vs. Irrational Numbers
Understanding the differences between rational and irrational numbers is essential for comprehending the full spectrum of real numbers. These differences highlight the unique properties and significance of each type of number.
Expression as Fractions
Rational numbers can be expressed as fractions, where both the numerator and the denominator are integers. In contrast, irrational numbers cannot be expressed in this manner, as their decimal expansions are infinite and non-repeating.
Decimal Representation
The decimal representation of rational numbers either terminates or repeats, while the decimal representation of irrational numbers is infinite and non-repeating. This distinction is a key factor in differentiating between the two types of numbers.
Density on the Number Line
Both rational and irrational numbers are densely packed on the real number line, but irrational numbers fill the gaps between rational numbers, ensuring the completeness of the line.
Frequently Asked Questions
What is an irrational number example?
An irrational number example is a number that cannot be expressed as a fraction of two integers. One of the most famous examples is Pi (π), which represents the ratio of a circle's circumference to its diameter.
Why are irrational numbers important?
Irrational numbers are important because they fill the gaps between rational numbers on the real number line, ensuring its continuity. They also have numerous applications in mathematics, science, and engineering.
How do you identify an irrational number?
An irrational number can be identified by its decimal expansion, which is infinite and non-repeating. Unlike rational numbers, irrational numbers cannot be expressed as a simple fraction.
Is the square root of 2 an irrational number?
Yes, the square root of 2 is an irrational number. It cannot be expressed as a simple fraction, and its decimal expansion is infinite and non-repeating.
Can irrational numbers be negative?
Yes, irrational numbers can be negative. For example, the negative square root of 2 is an irrational number. Irrational numbers can have both positive and negative values.
Are all irrational numbers transcendental?
No, not all irrational numbers are transcendental. While many irrational numbers, such as Pi and Euler's number, are transcendental, others, like the square root of 2, are not.
Conclusion
Irrational numbers are a fascinating and essential component of mathematics, bridging the gaps between rational numbers and ensuring the continuity of the real number line. From the enigmatic Pi to the aesthetically pleasing Golden Ratio, these numbers have captured the imagination of mathematicians and scientists for centuries. Their unique properties and applications continue to influence a wide range of fields, from geometry and calculus to art and design. By understanding and appreciating irrational numbers, we gain valuable insights into the intricate and beautiful world of mathematics.