Speed is a fundamental concept in physics, representing how quickly an object moves from one place to another. It's crucial not only in physics but also in everyday life, from calculating the time it takes for a car to reach its destination to determining the speed of a runner. Understanding the formula to calculate speed helps us make sense of motion and distance in a quantitative manner.

In this article, we'll delve into the intricacies of the formula to calculate speed and provide a thorough understanding of how it works. We'll explore the components of the formula, offer practical examples, and clarify common misconceptions. Whether you're a student, a teacher, or just someone interested in physics, this guide aims to enhance your comprehension of speed and its calculation.

By the end of this article, you'll be equipped with the knowledge to calculate speed accurately and efficiently. We'll also address frequently asked questions and provide additional resources for further exploration. So, let's dive into the fascinating world of speed and motion!

Understanding Speed
What is the Formula to Calculate Speed?
Components of the Speed Formula
How Does the Speed Formula Work?
Real-Life Applications of the Speed Formula
Common Misconceptions About Speed Calculation
Calculating Speed in Different Scenarios
How Can Speed Formula Be Used in Everyday Life?
Speed vs. Velocity: What's the Difference?
Advanced Speed Calculations
Tips for Accurate Speed Calculation
How Does Speed Affect Other Physical Quantities?
Frequently Asked Questions
Conclusion

Understanding Speed

Speed is defined as the rate at which an object covers distance. It is a scalar quantity, meaning it only has magnitude and no direction. Speed is typically measured in meters per second (m/s) or kilometers per hour (km/h). In physics, understanding speed is essential for solving problems related to motion, distance, and time.

Speed can be categorized into different types, such as average speed, instantaneous speed, and uniform speed. Average speed is calculated over a given distance, while instantaneous speed is the speed of an object at a specific moment. Uniform speed means the object is moving at a constant speed without any changes.

Grasping the concept of speed is crucial for students studying physics as it forms the foundation for more complex topics like velocity, acceleration, and momentum. It also plays a vital role in various real-world applications, such as transportation, sports, and engineering.

What is the Formula to Calculate Speed?

The formula to calculate speed is one of the most fundamental equations in physics. It is expressed as:

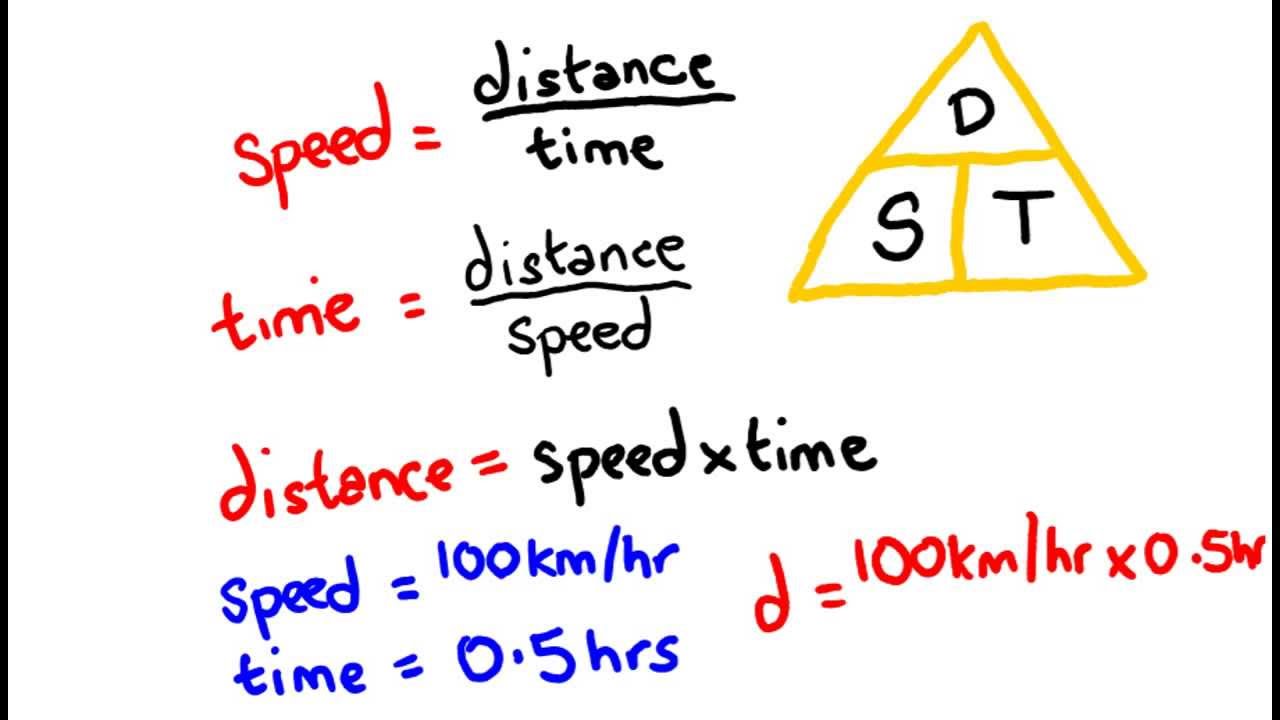
Speed = Distance / Time

This formula allows you to determine how fast an object is moving by dividing the distance it has traveled by the time it took to travel that distance. It provides a straightforward method to quantify motion and is applicable in numerous scenarios ranging from simple physics problems to complex engineering calculations.

Understanding this formula is crucial, as it forms the basis for more advanced calculations involving motion and helps solve real-life problems related to transportation, sports, and everyday activities. By mastering the formula to calculate speed, you can accurately determine the rate of motion for any object.

Components of the Speed Formula

The speed formula comprises three key components: speed, distance, and time. Each component plays a vital role in calculating how fast an object is moving. Let's break down these components:

Speed: This is the rate at which an object covers distance. It is a scalar quantity that measures how fast something is moving.
Distance: This refers to the total path covered by an object during its motion. It is typically measured in meters or kilometers.
Time: This is the duration taken by an object to cover a specific distance. It is usually measured in seconds, minutes, or hours.

To calculate speed accurately, it's essential to use consistent units for each component. For example, if you measure distance in kilometers, time should be measured in hours to obtain speed in km/h. Ensuring consistency in units is crucial for precise calculations and avoiding errors.

How Does the Speed Formula Work?

The speed formula works by providing a simple mathematical relationship between distance, time, and speed. By rearranging the formula, you can solve for different variables:

To find speed: Speed = Distance / Time
To find distance: Distance = Speed x Time
To find time: Time = Distance / Speed

Using this formula, you can determine any one of these variables if the other two are known. It serves as a practical tool for solving motion-related problems and understanding how different factors affect speed.

For instance, if a car travels 100 kilometers in 2 hours, you can calculate its speed by dividing the distance by time: Speed = 100 km / 2 hours = 50 km/h. This straightforward calculation allows you to quantify motion and make informed decisions based on the speed of an object.

Real-Life Applications of the Speed Formula

The speed formula has numerous real-life applications, making it a valuable tool in various fields. Here are some examples:

Transportation: Calculating the speed of vehicles helps in determining travel times, fuel efficiency, and safety measures.
Sports: Athletes use speed calculations to measure performance and improve training techniques.
Engineering: Engineers use speed calculations to design efficient transportation systems and machinery.
Astronomy: Scientists calculate the speed of celestial bodies to study their motion and predict their positions.

These applications demonstrate the versatility of the speed formula and its importance in both everyday life and specialized fields. By understanding how to calculate speed, you can make informed decisions and improve your understanding of motion-related phenomena.

Common Misconceptions About Speed Calculation

Despite its simplicity, the speed formula is often misunderstood, leading to common misconceptions. Here are some of the most frequent misunderstandings:

Speed and velocity are the same: While both measure motion, speed is a scalar quantity without direction, whereas velocity is a vector quantity with direction.
Average speed equals instantaneous speed: Average speed is the total distance divided by total time, while instantaneous speed is the speed at a specific moment.
Constant speed means constant velocity: An object can have a constant speed while changing direction, resulting in a changing velocity.

By clarifying these misconceptions, you can gain a more accurate understanding of speed and its calculation, allowing you to apply the formula more effectively in various scenarios.

Calculating Speed in Different Scenarios

Calculating speed can vary depending on the scenario. Here are some examples of how to apply the speed formula in different contexts:

Uniform motion: Calculate speed using the basic formula when an object moves at a constant speed without changes.
Non-uniform motion: Use average speed to account for variations in speed over a given distance.
Circular motion: Calculate the speed of an object moving in a circle by considering the circumference and time taken for one complete rotation.

By understanding these scenarios, you can choose the appropriate method for calculating speed and ensure accurate results in various situations.

How Can Speed Formula Be Used in Everyday Life?

The speed formula has practical applications in everyday life, helping us make informed decisions and improve efficiency. Here are some examples:

Travel planning: Calculate travel time and distance to plan efficient routes and avoid delays.
Fitness tracking: Measure running or cycling speed to monitor progress and set fitness goals.
Budgeting fuel: Estimate fuel consumption based on speed and distance to manage expenses.

These everyday applications highlight the importance of understanding and using the speed formula to enhance our daily lives and make informed decisions.

Speed vs. Velocity: What's the Difference?

Speed and velocity are often used interchangeably, but they have distinct differences. Here's a breakdown of these concepts:

Speed: A scalar quantity measuring how fast an object moves, without regard to direction.
Velocity: A vector quantity that includes both speed and direction, indicating how fast and in which direction an object is moving.

Understanding the difference between speed and velocity is crucial for accurately interpreting motion and making precise calculations in physics and real-world applications.

Advanced Speed Calculations

Advanced speed calculations often involve more complex scenarios, such as varying speeds, acceleration, and multi-step problems. Here are some techniques for tackling these calculations:

Use calculus: Apply calculus to calculate instantaneous speed and acceleration for varying speeds.
Break down multi-step problems: Divide complex problems into smaller steps, calculating speed for each segment before combining results.

By mastering these advanced techniques, you can solve more complex motion problems and deepen your understanding of speed and its calculation.

Tips for Accurate Speed Calculation

To ensure accurate speed calculations, consider the following tips:

Use consistent units: Ensure all measurements are in compatible units to avoid errors in calculations.
Double-check calculations: Verify calculations for accuracy and correct any mistakes.
Consider significant figures: Use appropriate significant figures to maintain precision in results.

By following these tips, you can enhance the accuracy of your speed calculations and make more informed decisions based on precise data.

How Does Speed Affect Other Physical Quantities?

Speed plays a significant role in influencing other physical quantities, such as:

Acceleration: Changes in speed directly affect acceleration, as it measures the rate of change of speed.
Momentum: Speed contributes to momentum, a measure of an object's motion based on its mass and velocity.
Kinetic energy: Speed impacts kinetic energy, as it is directly proportional to the square of speed.

Understanding how speed interacts with other physical quantities helps in analyzing motion and solving complex physics problems.

Frequently Asked Questions

What is the basic formula to calculate speed?
The basic formula to calculate speed is Speed = Distance / Time.
How can I calculate average speed?
To calculate average speed, divide the total distance traveled by the total time taken.
What units are used to measure speed?
Common units for measuring speed include meters per second (m/s) and kilometers per hour (km/h).
Can speed be negative?
No, speed is a scalar quantity and cannot be negative, as it only has magnitude, not direction.
How do I convert speed from km/h to m/s?
To convert speed from km/h to m/s, divide the speed by 3.6.
Is speed always constant?
No, speed can vary depending on factors like acceleration and external forces acting on the object.

Conclusion

In conclusion, understanding the formula to calculate speed is essential for interpreting motion and solving real-life problems. This comprehensive guide has equipped you with the knowledge to calculate speed accurately, apply it in various scenarios, and distinguish it from related concepts like velocity. By mastering the speed formula, you can enhance your understanding of motion and make informed decisions based on precise calculations. For further exploration, consider consulting additional resources or seeking expert guidance to deepen your knowledge of speed and its applications.

For more detailed information on physics and motion, you can explore resources like Khan Academy. This platform offers valuable insights and tutorials on various topics related to speed, velocity, and motion.