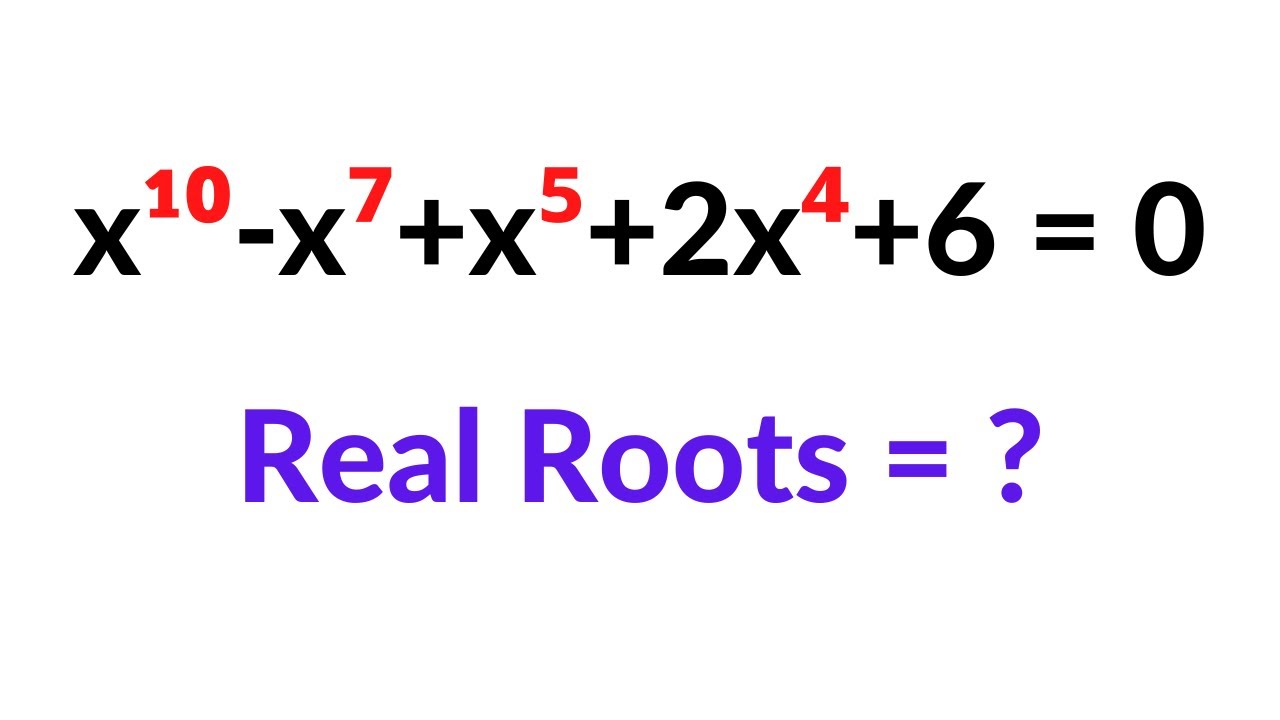Finding real roots is a fundamental concept in mathematics that often comes up in algebra and calculus. It refers to the solutions of an equation where the function equals zero. Real roots are crucial for understanding the behavior of polynomial functions, systems of equations, and even in real-world applications such as physics and engineering. But how do you go about finding these elusive solutions? This article is your complete guide to understanding and mastering the art of finding real roots, equipped with various methods and techniques to ensure success.
In this comprehensive guide, we'll dive deep into the various methods used to find real roots, covering everything from basic algebraic techniques to more advanced calculus-based approaches. Whether you're a student grappling with algebra homework or a professional dealing with complex equations, understanding how to find real roots is essential. We'll also explore common pitfalls, provide examples for clarity, and offer tips to make the process more intuitive.
Our aim is to provide an authoritative resource that not only explains the theory behind finding real roots but also offers practical, step-by-step instructions for applying these techniques. By the end of this article, you'll be equipped with the knowledge and tools needed to tackle any equation and find its real roots with confidence. Let's get started!
Table of Contents
- What Are Real Roots?
- Why Are Real Roots Important?
- Basic Methods for Finding Real Roots
- Graphical Methods for Root Finding
- Numerical Methods for Approximating Roots
- How to Use Technology to Find Roots?
- Common Mistakes to Avoid
- Real-World Applications of Real Roots
- How to Find Multiple Real Roots?
- Advanced Methods for Complex Equations
- How to Verify Your Solutions?
- FAQ on Finding Real Roots
- Conclusion
What Are Real Roots?
Real roots are the solutions of a polynomial equation where the function equals zero. In simpler terms, these are the values of the variable that make the overall equation true. For example, in the equation x^2 - 4 = 0, the real roots are x = 2 and x = -2. These roots can be either rational or irrational numbers, but they are always real numbers, as opposed to complex or imaginary numbers.
Why Are Real Roots Important?
Understanding real roots is critical because they provide insights into the behavior of functions. They tell us where the graph of a function intersects the x-axis, which is crucial for solving equations, modeling real-world phenomena, and optimizing processes. Moreover, knowing the real roots of a function helps in determining intervals of increase or decrease and identifying maximum or minimum points within those intervals.
Basic Methods for Finding Real Roots
There are several fundamental techniques for finding real roots, each with its advantages and suitable applications. In this section, we'll discuss some of the most common methods used in algebra and calculus.
Factoring Techniques
Factoring involves expressing a polynomial as a product of its factors, making it easier to identify the roots. For example, to find the roots of the equation x^2 - 5x + 6 = 0, we can factor it into (x - 2)(x - 3) = 0, giving us the roots x = 2 and x = 3. Factoring is particularly useful for quadratic equations and some cubic equations, where the roots are simple integers or fractions.
Using the Quadratic Formula
The quadratic formula is a robust tool for finding real roots of any quadratic equation. The formula is given by x = (-b ± √(b² - 4ac)) / (2a), where a, b, and c are coefficients of the equation ax² + bx + c = 0. The discriminant (b² - 4ac) determines the nature of the roots: if positive, there are two distinct real roots; if zero, there is one real root; and if negative, the roots are complex, indicating no real roots.
Graphical Methods for Root Finding
Graphical methods involve plotting the function on a graph and visually identifying the points where it intersects the x-axis. This method is intuitive and provides a clear picture of the function's behavior. By using graphing tools or software, you can quickly estimate the real roots and understand their distribution and multiplicity.
Numerical Methods for Approximating Roots
When algebraic techniques or graphical methods are insufficient, numerical methods can provide approximate solutions to finding real roots. These methods are particularly useful for complex or higher-degree polynomials.
Bisection Method
The bisection method is a simple and reliable technique for approximating real roots. It involves selecting an interval where the function changes sign and repeatedly halving the interval to zero in on the root. This iterative process continues until the desired degree of accuracy is achieved. The bisection method is slow but guarantees convergence to a real root if one exists within the interval.
Newton-Raphson Method
The Newton-Raphson method is a powerful technique for finding real roots, especially for differentiable functions. It uses the formula xₙ₊₁ = xₙ - f(xₙ) / f'(xₙ), which iteratively improves an initial guess to approximate the root. This method converges quickly if the initial guess is close to the actual root but may fail if the derivative is zero or if the function is not well-behaved near the root.
How to Use Technology to Find Roots?
With the advent of technology, finding real roots has become more accessible than ever. Graphing calculators, computer algebra systems, and specialized software offer tools for solving equations and visualizing functions. These technologies provide precise solutions and allow users to explore complex functions without manual calculations. Learning to leverage these tools effectively can greatly enhance your problem-solving capabilities.
Common Mistakes to Avoid
While finding real roots is a straightforward process, several common mistakes can lead to incorrect solutions. Some of these include:
- Ignoring the possibility of no real roots when the discriminant is negative.
- Failing to check all possible roots when using factoring techniques.
- Misinterpreting the graph when using graphical methods.
- Using inappropriate initial guesses in numerical methods, leading to divergence.
- Overlooking multiplicity when a root appears more than once.
Being aware of these pitfalls can help you avoid errors and achieve accurate results.
Real-World Applications of Real Roots
Real roots have numerous applications across various fields. In physics, they help solve motion and force equations, while in economics, they assist in finding equilibrium points in supply and demand models. Engineering relies on real roots to analyze stability and response of systems. Understanding these applications can provide context and motivation for mastering the techniques of root finding.
How to Find Multiple Real Roots?
In cases where an equation has multiple real roots, it's crucial to identify and verify each one. Techniques such as synthetic division and the Rational Root Theorem can help in systematically finding all possible roots. Additionally, considering the multiplicity of roots is essential for accurately describing the function's behavior.
Advanced Methods for Complex Equations
For equations that are too complex for basic algebraic techniques, advanced methods such as the Durand-Kerner method or the Bairstow's method can be employed. These methods are iterative and provide numerical approximations for the roots of polynomials of higher degrees. They require computational tools but offer solutions when traditional methods fall short.
How to Verify Your Solutions?
Once you've found the real roots of an equation, verifying their accuracy is crucial. Substituting the roots back into the original equation is a straightforward method to check if they satisfy the equation. Additionally, using graphing tools to confirm the intersection points and employing numerical approximation methods for cross-verification can ensure the reliability of your solutions.
FAQ on Finding Real Roots
- What is the difference between real and complex roots?
Real roots are solutions of an equation that are real numbers, whereas complex roots include imaginary numbers, which are not on the real number line.
- Can all equations have real roots?
No, not all equations have real roots. Some equations have complex roots, especially when the discriminant is negative.
- How do I know if a root is real or complex?
The discriminant (b² - 4ac) of a quadratic equation indicates the nature of the roots: positive for real roots, zero for a single real root, and negative for complex roots.
- What should I do if factoring doesn't work?
If factoring is not possible, try using the quadratic formula or numerical methods like the Newton-Raphson method for finding real roots.
- Are there tools to help find real roots?
Yes, graphing calculators, computer algebra systems, and software like MATLAB and Wolfram Alpha can assist in finding real roots.
- What is the role of technology in finding real roots?
Technology provides precise solutions, visualizes functions, and explores complex equations without manual calculations, enhancing problem-solving capabilities.
Conclusion
Finding real roots is a critical skill in mathematics, essential for solving equations and understanding the behavior of functions. By mastering various techniques—from basic algebraic methods to advanced numerical approaches—you can confidently tackle any equation. Remember to verify your solutions and utilize technology where applicable. With practice and perseverance, you'll become adept at finding real roots and applying these skills across various fields and real-world scenarios.
For further reading and resources, consider exploring online platforms like Khan Academy for tutorials and exercises on root finding techniques.