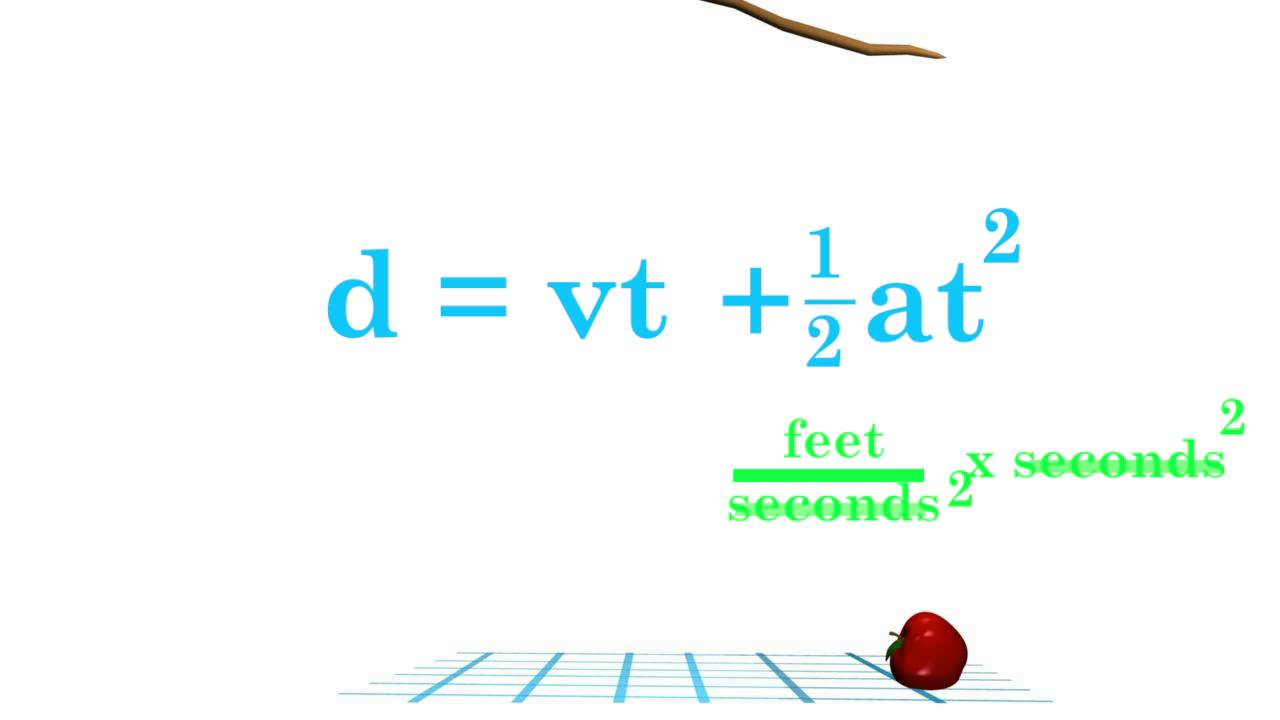Distance formula physics is a fundamental concept that bridges the gap between abstract theoretical principles and real-world applications. It's not just a mathematical expression; it's a powerful tool that helps us understand the dynamics of motion and space. Whether you're a seasoned physicist or a curious student, the distance formula is a key component in the study of physics, providing insights into how objects move and interact within the universe.
At its core, the distance formula is rooted in geometry and algebra, providing a straightforward method for calculating the distance between two points in a plane. This formula is essential in physics for analyzing motion, determining velocities, and understanding trajectories. The distance between two points is crucial in various applications, from engineering to astronomy. By exploring the principles of distance formula physics, we can gain a deeper appreciation for the intricacies of movement and space.
In this article, we'll delve into the nuances of distance formula physics, exploring its derivation, applications, and significance in various fields. We'll also address common questions and misconceptions, providing a comprehensive overview that enhances your understanding and appreciation of this essential physics tool. Whether you're seeking to deepen your knowledge or satisfy your curiosity, this guide is designed to illuminate the path of distance calculation in the realm of physics.
Table of Contents
- What is the Distance Formula in Physics?
- Derivation of the Distance Formula
- Applications of Distance Formula in Physics
- Distance Formula in 2D and 3D Space
- Role of Distance Formula in Kinematics
- How Does the Distance Formula Relate to Speed and Velocity?
- Distance Formula and Its Relevance in Astronomy
- Importance of Distance Formula in Engineering
- Real-World Scenarios Utilizing Distance Formula
- Limitations of the Distance Formula
- Can the Distance Formula Be Used in Relativity?
- Distance Formula in Daily Life
- Common Misconceptions About Distance Formula
- How to Overcome Challenges in Using Distance Formula?
- Frequently Asked Questions
- Conclusion
What is the Distance Formula in Physics?
The distance formula in physics is a mathematical equation used to calculate the distance between two points in a coordinate system. Typically expressed as \(d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\), it is derived from the Pythagorean theorem. In physics, this formula is crucial for understanding the spatial relationships between objects and is widely used in various branches, including classical mechanics and electromagnetism.
This formula provides a straightforward method for quantifying the separation between points in a two-dimensional plane but can also be extended to three dimensions. In three-dimensional space, the formula includes an additional component for the z-axis: \(d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}\). This extension is particularly useful in fields such as physics, where understanding the relative positions of objects in space is vital.
The distance formula is not just a theoretical construct; it is applied in real-world scenarios ranging from navigation systems to architectural design. By calculating precise distances, engineers and scientists can make informed decisions that impact the functionality and safety of their designs. Moreover, the distance formula forms the basis of more complex equations in physics, such as those used to determine speed, velocity, and acceleration.
Derivation of the Distance Formula
Understanding the derivation of the distance formula provides deeper insights into its significance in physics. The formula originates from the Pythagorean theorem, which relates the lengths of the sides of a right triangle. According to this theorem, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
To derive the distance formula, consider two points in a two-dimensional coordinate system: \(A(x_1, y_1)\) and \(B(x_2, y_2)\). By constructing a right triangle with these points, you can calculate the distance between them (the hypotenuse) using the Pythagorean theorem. The horizontal distance between the points is \((x_2 - x_1)\), and the vertical distance is \((y_2 - y_1)\). Thus, the distance formula becomes \(d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\).
In three-dimensional space, the derivation follows a similar process, with the addition of the z-axis component. The distance formula in 3D space is derived by considering the additional vertical distance \((z_2 - z_1)\), resulting in the formula: \(d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}\). This extension allows for the calculation of distances in a more comprehensive spatial context, essential for fields like physics and engineering.
Applications of Distance Formula in Physics
The distance formula is integral to various applications in physics, facilitating the understanding of motion, forces, and energy. It plays a pivotal role in classical mechanics, where it is used to determine the displacement of objects, calculate velocities, and analyze trajectories. By knowing the distance between two points, physicists can describe the motion of objects with greater precision.
In electromagnetism, the distance formula helps determine the strength of electric and magnetic fields. The intensity of these fields often depends on the separation between charges or current-carrying wires. By applying the distance formula, physicists can predict how these fields interact and influence objects within their vicinity.
Astronomy also benefits from the distance formula, particularly in the measurement of interstellar distances. Understanding the separation between celestial bodies is crucial for mapping the universe and studying the dynamics of galaxies. The distance formula aids astronomers in calculating light-years and other astronomical units, providing a framework for exploring the cosmos.
Distance Formula in 2D and 3D Space
The application of the distance formula in 2D and 3D spaces allows for comprehensive spatial analysis, essential in physics and related fields. In a two-dimensional coordinate system, the formula \(d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\) quantifies the distance between points on a plane, enabling calculations in various contexts, such as navigation and design.
When extended to three dimensions, the distance formula incorporates the z-axis, resulting in \(d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}\). This 3D version is particularly relevant in physics, where understanding the spatial relationships between objects is vital. For instance, in engineering, the 3D distance formula is used to design structures, ensuring their stability and functionality.
In fields like computer graphics and virtual reality, the distance formula is fundamental for rendering realistic environments. By calculating the distances between objects, software developers can create immersive experiences that mimic real-world physics. The versatility of the distance formula in both 2D and 3D spaces highlights its importance across various disciplines.
Role of Distance Formula in Kinematics
Kinematics, the branch of physics that deals with motion without considering forces, heavily relies on the distance formula to analyze and predict the movement of objects. By calculating the distance covered by an object over time, physicists can derive vital information about its velocity and acceleration.
In kinematic equations, the distance formula serves as the foundation for determining displacement, a vector quantity representing the change in position of an object. Displacement is crucial for understanding the overall motion, as it considers both the magnitude and direction of movement. By applying the distance formula, kinematic analyses become more precise and informative.
The distance formula also enables the study of projectile motion, where objects move in a curved trajectory under the influence of gravity. By calculating the horizontal and vertical components of distance, physicists can predict the path of projectiles, such as balls thrown into the air or rockets launched into space. This analysis is essential for fields like sports science and aerospace engineering.
How Does the Distance Formula Relate to Speed and Velocity?
The relationship between the distance formula and concepts like speed and velocity is fundamental in physics. Speed, a scalar quantity, represents the rate at which an object covers distance, while velocity, a vector quantity, includes direction in addition to speed.
To calculate average speed, the distance formula is used to determine the total distance traveled by an object over a specific period. The formula for average speed is \(speed = \frac{total\ distance}{total\ time}\). By knowing the distance, physicists can quantify how fast an object is moving, regardless of its direction.
In contrast, velocity requires both distance and direction. By using the distance formula to calculate displacement (the straight-line distance between the initial and final positions), velocity can be determined as \(velocity = \frac{displacement}{time}\). This distinction is crucial for understanding motion in physics, as velocity provides a more comprehensive view of an object's movement.
Distance Formula and Its Relevance in Astronomy
Astronomy, the study of celestial objects and phenomena, relies heavily on the distance formula to measure the vast expanses of space. Accurately calculating the separation between stars, planets, and galaxies is essential for understanding the universe's structure and evolution.
The distance formula allows astronomers to determine distances in light-years, the unit of distance that light travels in a year. By measuring the apparent brightness and using parallax methods, astronomers can estimate the distance to stars and other celestial bodies. These calculations provide insights into the size and composition of the universe, contributing to our understanding of cosmology.
In addition to measuring distances within our galaxy, the distance formula is instrumental in calculating the expansion rate of the universe. By analyzing the redshift of distant galaxies, astronomers can determine how quickly they are moving away from us, a key factor in understanding the Big Bang theory and the universe's ongoing expansion.
Importance of Distance Formula in Engineering
Engineering, the application of scientific principles to design and build structures, machines, and systems, frequently employs the distance formula to ensure precision and accuracy. In civil engineering, the formula is used to calculate distances in construction projects, such as roads, bridges, and buildings, ensuring they meet safety and functionality standards.
Mechanical engineers use the distance formula to analyze the movement of components within machines. By understanding the distances between parts, engineers can design efficient systems that minimize wear and maximize performance. This analysis is crucial for developing reliable and durable machinery.
In electrical engineering, the distance formula aids in designing circuits and networks. By calculating the distances between components, engineers can optimize the layout of electrical systems, improving efficiency and reducing energy loss. The formula is also used in telecommunications, where it helps determine the optimal placement of antennas and transmitters for signal coverage.
Real-World Scenarios Utilizing Distance Formula
The distance formula is not limited to theoretical applications; it is used in numerous real-world scenarios that impact our daily lives. In navigation, the formula helps determine the shortest path between two locations, essential for GPS systems and route planning. By calculating distances accurately, these systems provide efficient and reliable directions.
In sports, the distance formula is used to measure performance metrics, such as the distance a runner covers in a race or the trajectory of a golf ball. These calculations enable athletes and coaches to analyze and improve performance, contributing to the advancement of sports science.
In architecture and urban planning, the distance formula is used to design and organize spaces. By calculating the distances between structures, architects can create efficient layouts that maximize space and accessibility. This analysis is vital for developing functional and aesthetically pleasing environments.
Limitations of the Distance Formula
While the distance formula is a powerful tool in physics and other fields, it has limitations that must be considered. The formula assumes a straight-line distance between points, which may not always be applicable in real-world scenarios where paths are curved or irregular.
In addition, the distance formula does not account for changes in elevation or terrain, factors that can significantly impact actual distances. For instance, in mountainous regions, the formula may underestimate the true distance between points, affecting navigation and planning accuracy.
Moreover, the distance formula is based on Euclidean geometry, which assumes a flat, two-dimensional plane. In curved spaces, such as those described by general relativity, the formula may not accurately reflect the true distances between points. In these cases, more complex mathematical models are required to account for the curvature of space-time.
Can the Distance Formula Be Used in Relativity?
In the context of Einstein's theory of relativity, the distance formula's application is limited due to the curvature of space-time. In general relativity, gravity is not viewed as a force but as a curvature of space-time caused by mass. This curvature affects the paths of objects, requiring non-Euclidean geometry to describe distances accurately.
While the distance formula provides a useful approximation in flat, Euclidean spaces, it must be modified or replaced in curved space-time. In relativity, the concept of distance is generalized to include the effects of gravity, using more complex mathematical constructs like tensors and metrics to describe the geometry of space-time.
Despite its limitations, the distance formula remains valuable in special relativity, where space-time is considered flat, and the effects of gravity are negligible. In this context, the formula can be used to calculate distances and analyze motion in inertial reference frames, providing insights into phenomena like time dilation and length contraction.
Distance Formula in Daily Life
The distance formula's applications extend beyond scientific and technical fields, influencing various aspects of our daily lives. In education, the formula is a staple of mathematics and physics curricula, teaching students essential problem-solving skills and spatial reasoning.
In transportation, the distance formula helps optimize routes and schedules, improving efficiency and reducing travel time. By calculating distances accurately, logistics companies can plan deliveries and shipments, ensuring timely and cost-effective operations.
The distance formula also plays a role in personal fitness, where it is used to track distances covered during exercise. Fitness apps and devices use the formula to calculate metrics like speed and calories burned, helping individuals monitor and achieve their health goals.
Common Misconceptions About Distance Formula
Several misconceptions about the distance formula can lead to misunderstandings in its application and interpretation. One common misconception is that the formula only applies to flat, two-dimensional spaces. While it is derived from Euclidean geometry, the distance formula can be adapted for use in three-dimensional and even curved spaces with modifications.
Another misconception is that the distance formula accounts for all factors affecting distance, such as elevation and terrain. In reality, the formula provides a straight-line distance, requiring additional calculations or adjustments for more complex scenarios.
Some people mistakenly believe that the distance formula is only relevant in academic settings, overlooking its practical applications in everyday life. From navigation and engineering to sports and fitness, the distance formula is a versatile tool with widespread utility.
How to Overcome Challenges in Using Distance Formula?
Overcoming challenges in using the distance formula involves understanding its limitations and adapting it to suit specific contexts. For scenarios involving curved paths or irregular terrain, additional calculations or alternative methods may be necessary to obtain accurate results.
In cases where elevation or terrain significantly impacts distance, incorporating topographical data or using geographic information systems (GIS) can enhance accuracy. These tools provide detailed maps and models that account for variations in the landscape, improving distance calculations.
For applications involving curved space-time, such as in general relativity, using more advanced mathematical models like tensors and metrics can address the limitations of the distance formula. These models provide a comprehensive framework for describing distances in curved spaces, accommodating the effects of gravity and mass.
Frequently Asked Questions
1. What is the primary use of the distance formula in physics?
The primary use of the distance formula in physics is to calculate the distance between two points in space, essential for analyzing motion, determining velocities, and understanding trajectories.
2. How does the distance formula apply in three-dimensional space?
In three-dimensional space, the distance formula extends to include a z-axis component, allowing for the calculation of distances between points in a more comprehensive spatial context.
3. Can the distance formula be used in non-Euclidean geometry?
While the distance formula is based on Euclidean geometry, it can be adapted or replaced with more complex models to account for curved spaces, as seen in general relativity.
4. What are some real-world applications of the distance formula?
Real-world applications of the distance formula include navigation, sports performance analysis, architectural design, and engineering, where accurate distance calculations are essential.
5. How is the distance formula used in astronomy?
In astronomy, the distance formula helps measure interstellar distances, calculate light-years, and analyze the expansion rate of the universe, contributing to our understanding of cosmology.
6. What are common misconceptions about the distance formula?
Common misconceptions include the belief that the formula is only applicable in flat spaces, accounts for all distance-affecting factors, and is limited to academic settings.
Conclusion
The distance formula is a cornerstone of physics and mathematics, providing a reliable method for calculating the separation between points in space. Its applications span various fields, from engineering and astronomy to daily life, highlighting its versatility and importance. By understanding the principles and limitations of the distance formula, we can harness its power to solve complex problems and explore the mysteries of the universe.
Whether used in academic research, engineering projects, or everyday scenarios, the distance formula remains an essential tool for understanding the dynamics of motion and space. By mastering its application, we can unlock new opportunities for innovation and discovery, paving the way for advancements in science and technology.